题目内容
15. 如图,在△ABC中,D、F、E分别为边BC、AB、AC上的一点,连接BE、FD,它们相交于点G,连接DE,若四边形AFDE是平行四边形,则下列说法正确的是( )
如图,在△ABC中,D、F、E分别为边BC、AB、AC上的一点,连接BE、FD,它们相交于点G,连接DE,若四边形AFDE是平行四边形,则下列说法正确的是( )| A. | $\frac{FG}{GD}=\frac{BF}{AF}$ | B. | $\frac{AE}{AC}=\frac{BF}{AF}$ | C. | $\frac{FG}{AE}=\frac{BF}{AF}$ | D. | $\frac{CE}{EA}=\frac{BF}{AF}$ |
分析 由四边形AFDE是平行四边形,可得AE∥DF,DE∥AB,DE=AF,根据平行线分线段成比例定理与相似三角形的对应边成比例,即可求得答案.
解答 解:A、∵四边形AFDE是平行四边形,
∴AE∥DF,DE∥AB,DE=AF,
∴△BFG∽△EDG,
∴$\frac{FG}{GD}=\frac{BF}{DE}$,
∴$\frac{FG}{GD}=\frac{BF}{AF}$,故正确;
B、∵$\frac{AE}{AC}=\frac{BD}{BC}$,$\frac{BD}{BC}=\frac{BF}{AB}$,
∴$\frac{AE}{AC}=\frac{BF}{AB}$,故错误;
C、∵DF∥AC,
∴$\frac{FG}{AE}=\frac{BF}{AB}$,故错误;
D、∵$\frac{CE}{EA}=\frac{CD}{BD}$,$\frac{CD}{BD}=\frac{AF}{BF}$,
∴$\frac{CE}{EA}$=$\frac{AF}{BF}$.故错误.
故选A.
点评 此题考查了相似三角形的判定与性质以及平行线分线段成比例定理.注意掌握各线段的对应关系是解此题的关键.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
5. 如图,正方形ABCD的边长为2,AE=EB,MN=1,线段MN的两端在CB、CD上滑动,当△AED与N、M、C为顶点的三角形相似时,CM的长为( )
如图,正方形ABCD的边长为2,AE=EB,MN=1,线段MN的两端在CB、CD上滑动,当△AED与N、M、C为顶点的三角形相似时,CM的长为( )
 如图,正方形ABCD的边长为2,AE=EB,MN=1,线段MN的两端在CB、CD上滑动,当△AED与N、M、C为顶点的三角形相似时,CM的长为( )
如图,正方形ABCD的边长为2,AE=EB,MN=1,线段MN的两端在CB、CD上滑动,当△AED与N、M、C为顶点的三角形相似时,CM的长为( )| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{\sqrt{5}}{5}$或$\frac{2\sqrt{5}}{5}$ | D. | $\frac{1}{5}$ |
 已知:如图,线段AB=12cm,M是AB上一定点,C、D两点分别从M、B出发以1cm/s、3cm/s的速度沿线段BA向左运动,在运动过程中,点C始终在线段AM上,点D始终在线段BM上,点E、F分别是线段AC和MD的中点.
已知:如图,线段AB=12cm,M是AB上一定点,C、D两点分别从M、B出发以1cm/s、3cm/s的速度沿线段BA向左运动,在运动过程中,点C始终在线段AM上,点D始终在线段BM上,点E、F分别是线段AC和MD的中点.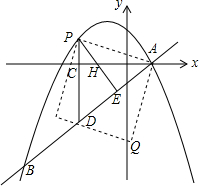 如图,在平面直角坐标系中,直线y=kx+n(k≠0)与抛物线y=-$\frac{1}{4}{x^2}$+bx+c交于A、B两点,点A在x轴上,OA=2,点B的横坐标为-8,且tan∠OAB=$\frac{3}{4}$.
如图,在平面直角坐标系中,直线y=kx+n(k≠0)与抛物线y=-$\frac{1}{4}{x^2}$+bx+c交于A、B两点,点A在x轴上,OA=2,点B的横坐标为-8,且tan∠OAB=$\frac{3}{4}$. 如图,点A为直线y=-x上一点,过A作OA的垂线交双曲线y=$\frac{k}{x}$(x<0)于点B,若OA2-AB2=12,则k的值为-6.
如图,点A为直线y=-x上一点,过A作OA的垂线交双曲线y=$\frac{k}{x}$(x<0)于点B,若OA2-AB2=12,则k的值为-6. 看图.项空:
看图.项空:


