题目内容
8．计算：（1）（3a+b）2；
（2）（2a+$\frac{1}{3}$b）2；
（3）（2a-4b）2；
（4）（$\frac{1}{2}$a-$\frac{1}{3}$b）2．
分析 （1）直接利用完全平方公式计算得出即可；
（2）直接利用完全平方公式计算得出即可；
（3）直接利用完全平方公式计算得出即可；
（4）直接利用完全平方公式计算得出即可．
解答 解：（1）（3a+b）2=9a2+6ab+b2；
（2）（2a+$\frac{1}{3}$b）2；=4a2+$\frac{4}{3}$ab+$\frac{1}{9}$2；
（3）（2a-4b）2=4a2+16b2-16ab；
（4）（$\frac{1}{2}$a-$\frac{1}{3}$b）2=$\frac{1}{4}$a2+$\frac{1}{9}$b2-$\frac{1}{3}$ab．
点评 此题主要考查了完全平方公式，正确掌握完全平方公式的基本形式是解题关键．
练习册系列答案
第三学期赢在暑假系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
相关题目
18．在方程$\frac{2}{3}$x+1=$\frac{1}{2}$的两边同时乘以6，得（ ）
| A． | 4x+1=3 | B． | 2x+6=3 | C． | 4x+3=3 | D． | 4x+6=3 |
19．
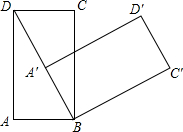如图，矩形ABCD中，AB=1，AD=$\sqrt{3}$，若矩形ABCD以B为中心，按顺时针方向旋转到A′B′C′D′的位置（点A′落在对角线BD上），则对角线BD扫过的图形的面积为（ ）
如图，矩形ABCD中，AB=1，AD=$\sqrt{3}$，若矩形ABCD以B为中心，按顺时针方向旋转到A′B′C′D′的位置（点A′落在对角线BD上），则对角线BD扫过的图形的面积为（ ）| A． | $\frac{π}{3}$ | B． | $\frac{2π}{3}$ | C． | π | D． | $\frac{4π}{3}$ |
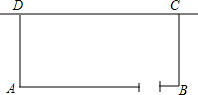现有长28米的网，围成一个一面靠墙的矩形鸡舍：已知墙长14米，AB边可开一个或两个1米宽的门．
在Rt△ABC中，∠C=90°，AD平分∠ACB，AC=10cm，AB=26cm，求BD的长．
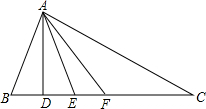如图，