题目内容
19.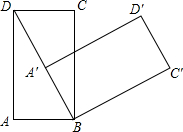 如图,矩形ABCD中,AB=1,AD=$\sqrt{3}$,若矩形ABCD以B为中心,按顺时针方向旋转到A′B′C′D′的位置(点A′落在对角线BD上),则对角线BD扫过的图形的面积为( )
如图,矩形ABCD中,AB=1,AD=$\sqrt{3}$,若矩形ABCD以B为中心,按顺时针方向旋转到A′B′C′D′的位置(点A′落在对角线BD上),则对角线BD扫过的图形的面积为( )| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | π | D. | $\frac{4π}{3}$ |
分析 根据旋转的性质可知∠DBD′=∠ABD,由AB=1,AD=$\sqrt{3}$,可知BD=2,∠ABD=60°,根据扇形的面积公式计算即可.
解答 解:∵矩形ABCD中,AB=1,AD=$\sqrt{3}$,
∴BD=2,∠ABD=60°,
根据旋转的性质可知∠DBD′=∠ABD=60°,
∴S扇形DBD′=$\frac{60×π×{2}^{2}}{360}$=$\frac{2π}{3}$,
故选B.
点评 本题主要考查了旋转的性质和扇形的面积计算,熟悉旋转的性质求出扇形的圆心角是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.某学校新建阶梯教室,第一排有25个座位,后面每排都比前一排多一个座位,若第n排有m个座位,教室共有p个座位.
(1)写出m与n,p与n之间的函数式;
(2)若教室座位共有15排,座位总数将达到多少个?
(1)写出m与n,p与n之间的函数式;
(2)若教室座位共有15排,座位总数将达到多少个?
4. 如图,AD⊥BC于D,DE是△ADC的中线,则以AD为高的三角形有( )
如图,AD⊥BC于D,DE是△ADC的中线,则以AD为高的三角形有( )
 如图,AD⊥BC于D,DE是△ADC的中线,则以AD为高的三角形有( )
如图,AD⊥BC于D,DE是△ADC的中线,则以AD为高的三角形有( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
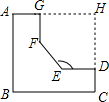 一个零件的形状如图所示,按规定∠A=∠B=∠C=∠D=∠G=90°,∠E=140°,质检工人测得∠F=140°,就断定这个零件不合格,这是为什么?
一个零件的形状如图所示,按规定∠A=∠B=∠C=∠D=∠G=90°,∠E=140°,质检工人测得∠F=140°,就断定这个零件不合格,这是为什么? 如图,在△ABC中,∠BAC=90°,∠1=∠2.AM⊥BC于点M,AD⊥BE于点F,交BC于点D,AM交BE于点G.求证:∠2=∠3=∠4.
如图,在△ABC中,∠BAC=90°,∠1=∠2.AM⊥BC于点M,AD⊥BE于点F,交BC于点D,AM交BE于点G.求证:∠2=∠3=∠4.