题目内容
17. 公交总站(A点)与B、C两个站点的位置如图所示,已知AC=6km,∠B=30°,∠C=15°,求B站点离公交总站的距离即AB的长(结果保留根号).
公交总站(A点)与B、C两个站点的位置如图所示,已知AC=6km,∠B=30°,∠C=15°,求B站点离公交总站的距离即AB的长(结果保留根号).
分析 过C作CD垂直于AB,交BA延长线于点D,由∠B与∠ACB的度数,利用外角性质求出∠CAD的度数,在直角三角形ACD中,利用勾股定理求出CD与AD的长,在直角三角形BCD中,利用勾股定理求出BD的长,由BD-AD求出AB的长即可.
解答 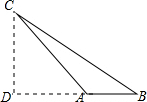 解:过点C作CD⊥AB,垂足为点D,
解:过点C作CD⊥AB,垂足为点D,
∵∠B=30°,∠ACB=15°,
∴∠CAD=45°,
在Rt△ACD中,∠ADC=90°,∠CAD=45°,AC=6,
∴CD=AD=3$\sqrt{2}$km,
在Rt△BCD中,∠CDB=90°,∠B=30°,CD=3$\sqrt{2}$km,
∴BD=3$\sqrt{6}$km,
则AB=(3$\sqrt{6}$-3$\sqrt{2}$)km.
点评 此题考查了解直角三角形的应用,熟练掌握勾股定理是解本题的关键.

练习册系列答案
相关题目
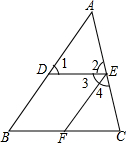 如图,在三角形ABC中,D、E分别是AB、AC边上的点,∠A=50°,∠1=60°,∠4=50°,∠BFE=120°.
如图,在三角形ABC中,D、E分别是AB、AC边上的点,∠A=50°,∠1=60°,∠4=50°,∠BFE=120°. 如图,直线y=k1x+b1与y=k2x+b2相交于点A(-2,0),与y轴分别交于点B、C,且与y轴围成的△ABC的面积为4,求b1-b2的值.
如图,直线y=k1x+b1与y=k2x+b2相交于点A(-2,0),与y轴分别交于点B、C,且与y轴围成的△ABC的面积为4,求b1-b2的值. 如图,已知P为⊙O外一点,连结OP交⊙O于点A,且OA=2AP,求作直线PB,使PB与⊙O相切.以下是甲、乙两同学的作业.
如图,已知P为⊙O外一点,连结OP交⊙O于点A,且OA=2AP,求作直线PB,使PB与⊙O相切.以下是甲、乙两同学的作业.