题目内容
7.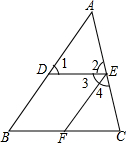 如图,在三角形ABC中,D、E分别是AB、AC边上的点,∠A=50°,∠1=60°,∠4=50°,∠BFE=120°.
如图,在三角形ABC中,D、E分别是AB、AC边上的点,∠A=50°,∠1=60°,∠4=50°,∠BFE=120°.(1)求∠2的度数;
(2)求证:DE∥BC;
(3)求证:∠3=∠B.
分析 (1)根据三角形的内角和定理得出∠2的度数即可;
(2)先证∠3的度数,再由∠BFE=120°,得出DE∥BC;
(3)由平行线的判定得DB∥EF,求得∠B,即可得出∠3=∠B.
解答 解:(1)∵∠A+∠1+2=180°,∠A=50°,∠1=60°,
∴∠2=180°-50°-60°=70°;
(2)∵∠4=50°,
∴∠3=60°,
∵∠BFE=120°,
∴∠3+∠BFE=180°,
∴DE∥BC;
(3)∵∠A=50°,∠4=50°,
∴∠A=∠4,
∴DB∥EF,
∴∠B=60°,
∴∠3=∠B.
点评 本题考查了平行线的判定和性质,掌握平行线的判定方法是解题的关键.

练习册系列答案
相关题目
12. 如图,点A在直线l1上,点B,C分别在直线l2上,AB⊥l2,AC⊥l1,AB=4,BC=3,则下列说法正确的是( )
如图,点A在直线l1上,点B,C分别在直线l2上,AB⊥l2,AC⊥l1,AB=4,BC=3,则下列说法正确的是( )
 如图,点A在直线l1上,点B,C分别在直线l2上,AB⊥l2,AC⊥l1,AB=4,BC=3,则下列说法正确的是( )
如图,点A在直线l1上,点B,C分别在直线l2上,AB⊥l2,AC⊥l1,AB=4,BC=3,则下列说法正确的是( )| A. | 点B到直线 l1的距离等于4 | B. | 点C到直线l1的距离等于5 | ||
| C. | 直线l1,l2的距离等于4 | D. | 点B到直线AC的距离等于3 |
19. 如图,下列条件中能够判断出AB∥CD的是( )
如图,下列条件中能够判断出AB∥CD的是( )
 如图,下列条件中能够判断出AB∥CD的是( )
如图,下列条件中能够判断出AB∥CD的是( )| A. | ∠A=∠C | B. | ∠B=∠D | C. | ∠A+∠B=180° | D. | ∠A+∠D=180° |
 在一次抓捕贩毒分子的行动中,一贩毒分子从两条公路的交点O处沿到两条公路OM、ON距离相等的一条小路上逃窜(如图所示,在∠MON内),埋伏在A、B两处的公安人员想在相等的距离同时抓住贩毒分子(两处公安人员速度相同),请你帮助公安人员在图中标出抓捕点P的位置(不写作法,保留作图痕迹).
在一次抓捕贩毒分子的行动中,一贩毒分子从两条公路的交点O处沿到两条公路OM、ON距离相等的一条小路上逃窜(如图所示,在∠MON内),埋伏在A、B两处的公安人员想在相等的距离同时抓住贩毒分子(两处公安人员速度相同),请你帮助公安人员在图中标出抓捕点P的位置(不写作法,保留作图痕迹).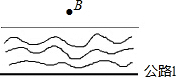 如图,河边有一条笔直的公路l,公路两侧是平坦的草地,在数学活动课上,老师要求测量河对岸B点到公路的距离,请你设计一个测量方案.要求:
如图,河边有一条笔直的公路l,公路两侧是平坦的草地,在数学活动课上,老师要求测量河对岸B点到公路的距离,请你设计一个测量方案.要求: 如图,E、F是?ABCD对角线AC上的两点,AF=CE.
如图,E、F是?ABCD对角线AC上的两点,AF=CE. 公交总站(A点)与B、C两个站点的位置如图所示,已知AC=6km,∠B=30°,∠C=15°,求B站点离公交总站的距离即AB的长(结果保留根号).
公交总站(A点)与B、C两个站点的位置如图所示,已知AC=6km,∠B=30°,∠C=15°,求B站点离公交总站的距离即AB的长(结果保留根号).