题目内容
15.己知函数y=(m+2)${x}^{{m}^{2}+m-4}$是关于x的二次函数.求:(1)满足条件的m的值;
(2)m为何值时,抛物线有最低点?求出这个最低点,这时,抛物线的开口方向、增减性如何?
分析 (1)根据二次函数的定义求出m的值即可解决问题.
(2)运用当二次项系数大于0时,抛物线开口向上,图象有最低点;在对称轴的右侧y随x的增大而增大.
解答 解:(1)根据题意,m2+m-4=2且m+2≠0,
解得:m=2或m=-3;
(2)当m=-3时,m+2=-1<0,抛物线开口向下,无最低点;
当m=2时,抛物线解析式为:y=4x2,
知该抛物线有最低点,最低点坐标为(0,0),
这时抛物线开口向上,当x<0时,y随x的增大而减小;当x>0时,y随x的增大而增大.
点评 该题主要考查了二次函数的定义及其性质的应用问题;牢固掌握定义及其性质是解题的关键.

练习册系列答案
相关题目
20.直线y=2x+1与直线y=-3x+6交于点(a,b),则$\left\{\begin{array}{l}{x=a}\\{y=b}\end{array}\right.$是方程组( )的解.
| A. | $\left\{\begin{array}{l}{y=2x+1}\\{y=-3x}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{y=2x+1}\\{y=-3x+6}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{y=2x+1}\\{y=3x+6}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{y=2x-1}\\{y=-3x+6}\end{array}\right.$ |
7.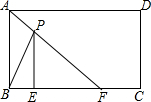 如图,在矩形ABCD中,AB=4cm,AD=5cm.点E在BC边上,且BE=1cm,AF平分∠BAD.图中P为AF上任意一点,若P为AF上任意一动点,请确定一点P,连接BP、EP,则BP+EP的最小值为( )
如图,在矩形ABCD中,AB=4cm,AD=5cm.点E在BC边上,且BE=1cm,AF平分∠BAD.图中P为AF上任意一点,若P为AF上任意一动点,请确定一点P,连接BP、EP,则BP+EP的最小值为( )
 如图,在矩形ABCD中,AB=4cm,AD=5cm.点E在BC边上,且BE=1cm,AF平分∠BAD.图中P为AF上任意一点,若P为AF上任意一动点,请确定一点P,连接BP、EP,则BP+EP的最小值为( )
如图,在矩形ABCD中,AB=4cm,AD=5cm.点E在BC边上,且BE=1cm,AF平分∠BAD.图中P为AF上任意一点,若P为AF上任意一动点,请确定一点P,连接BP、EP,则BP+EP的最小值为( )| A. | 4cm | B. | 5cm | C. | 4$\sqrt{2}$cm | D. | 3cm |
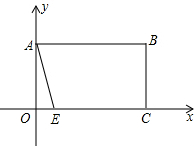 如图,在平面直角坐标系中,四边形OABC是矩形,其中点B的坐标为(5,3),点E在x轴上,将矩形OABC沿AE折叠,点B恰好落在x轴上,求折痕的解析式.
如图,在平面直角坐标系中,四边形OABC是矩形,其中点B的坐标为(5,3),点E在x轴上,将矩形OABC沿AE折叠,点B恰好落在x轴上,求折痕的解析式.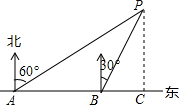 如图,小聪同学在东西走向的文一路A处,测得一处公共自行车租用服务点P在北偏东60°方向上,在A处往东90米的B处,又测得该服务点P在北偏东30°方向上,则该服务点P到文一路的距离PC为45$\sqrt{3}$.
如图,小聪同学在东西走向的文一路A处,测得一处公共自行车租用服务点P在北偏东60°方向上,在A处往东90米的B处,又测得该服务点P在北偏东30°方向上,则该服务点P到文一路的距离PC为45$\sqrt{3}$.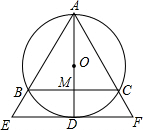 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,AD与BC相交于点M,且BM=MC,过点D作BC的平行线,分别与AB、AC的延长线相交于点E、F.
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,AD与BC相交于点M,且BM=MC,过点D作BC的平行线,分别与AB、AC的延长线相交于点E、F.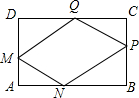 在一块矩形ABCD的空地上划一块平行四边形MNPQ进行绿化.如图,平行四边形MNPQ的顶点在矩形的边长,且AM=CP=xm,∠ANM=∠CQP=30°.已知矩形的边BC=100m,边AB=am,a为大于100的常数,设四边形MNPQ的面积为Sm2.
在一块矩形ABCD的空地上划一块平行四边形MNPQ进行绿化.如图,平行四边形MNPQ的顶点在矩形的边长,且AM=CP=xm,∠ANM=∠CQP=30°.已知矩形的边BC=100m,边AB=am,a为大于100的常数,设四边形MNPQ的面积为Sm2.