题目内容
3.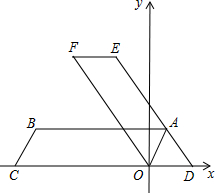 如图,四边形ABCO是平行四边形,OA=2,AB=6,点C在x轴的负半轴上,将?ABCO绕点O顺时针旋转α°(0<α<90°)得到?DEFO,点A的对应点点D恰好落在x轴的正半轴上,且DE经过点A.
如图,四边形ABCO是平行四边形,OA=2,AB=6,点C在x轴的负半轴上,将?ABCO绕点O顺时针旋转α°(0<α<90°)得到?DEFO,点A的对应点点D恰好落在x轴的正半轴上,且DE经过点A.(1)若点F在反比例函数y=$\frac{k}{x}$(x<0)的图形上,求α及k的值.
(2)求旋转过程中?ABCO扫过的面积.
分析 (1)作FG⊥x轴于G.求出点F的坐标即可解决问题.
(2)由图象可知,平行四边形ABCO扫过的面积可由扇形OCF、平行四边形ABCO、扇形OAD的面积之和减去△OAD的面积得到,分别计算即可.
解答 解:(1)作FG⊥x轴于G.
∵四边形ABCO是平行四边形,
∴AB∥CO,
∵OD∥AB,∠AOD=α°,
∴∠BAO=∠DOA=α°,
∵?ABCO绕点O顺时针旋转α°(0<α<90°)得到?DEFO,
∴∠BAO=∠ODA=α°,
∵OA=OD,
∴∠OAD=∠ODA=α°,
在△AOD中,α°+α°+α°=180°,
∴α=60,
∵OF=6,
∴OG=3,FG=3$\sqrt{3}$,
∵F在第二象限,
∴F(-3,3$\sqrt{3}$),
∵y=$\frac{k}{x}$经过点F,
∴k=-9$\sqrt{3}$.
(2)由图象可知,平行四边形ABCO扫过的面积可由扇形OCF、平行四边形ABCO、扇形OAD的面积之和减去△OAD的面积得到,
∵OC=6,α=60,
∴S扇形OCF=$\frac{60•π•{6}^{2}}{360}$=6π,
∵BC=2,
∴平行四边形ABCO的BC边上的高为$\sqrt{3}$,
∴S平行四边形ABCO=6$\sqrt{3}$,
∵OA=2,
∴S扇形OAD=$\frac{60•π•{2}^{2}}{360}$=$\frac{2}{3}$π,S△AOD=$\frac{1}{2}$•2$•\sqrt{3}$=$\sqrt{3}$,
∴S=6$π+6\sqrt{3}$+$\frac{2}{3}$π-$\sqrt{3}$=$\frac{20}{3}$π+5$\sqrt{3}$.
点评 本题考查反比例函数的性质、旋转变换、平行四边形的性质、扇形的面积公式、坐标与图形的性质等知识,解题的关键是学会利用分割法求面积,属于中考常考题型.

| A. | 4x-3(-9-3x)=3 | B. | 4x+3(-9-3x)=3 | C. | 4x-3(-9+3x)=3 | D. | 4x+3(-9+3x)=3 |
| A. | 图象经过(1,-1) | B. | 图象位于二、四象限 | ||
| C. | 图象是中心对称图形 | D. | y随x的增大而减小 |
| A. | a=1,b=-6 | B. | a=5,b=6 | C. | a=1,b=6 | D. | a=5,b=-6 |
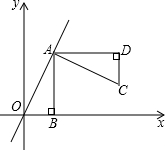 如图,正比例函数y=kx经过点A(2,4),AB⊥x轴于点B.
如图,正比例函数y=kx经过点A(2,4),AB⊥x轴于点B.
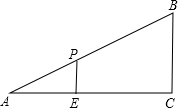 如图,在△ABC中,∠C=90°,∠A=30°,BC=3,P是AB上的一动点,PE⊥AC于E,沿PE将∠A折叠,点A的对应点为D,若△BPD是直角三角形,则PA=2或4.
如图,在△ABC中,∠C=90°,∠A=30°,BC=3,P是AB上的一动点,PE⊥AC于E,沿PE将∠A折叠,点A的对应点为D,若△BPD是直角三角形,则PA=2或4.