题目内容
8.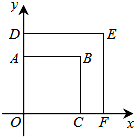 如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,相似比为1:$\sqrt{2}$,点B的坐标为(1,1),则点E的坐标是($\sqrt{2}$,$\sqrt{2}$).
如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,相似比为1:$\sqrt{2}$,点B的坐标为(1,1),则点E的坐标是($\sqrt{2}$,$\sqrt{2}$).
分析 根据位似变换的概念、相似多边形的概念计算即可.
解答 解:∵正方形OABC与正方形ODEF是位似图形,点O为位似中心,相似比为1:$\sqrt{2}$,点B的坐标为(1,1),
∴$\frac{AO}{OD}$=$\frac{1}{\sqrt{2}}$,$\frac{OC}{OF}$=$\frac{1}{\sqrt{2}}$,
∴点E的坐标是($\sqrt{2}$,$\sqrt{2}$),
故答案为:$\sqrt{2}$;$\sqrt{2}$.
点评 本题考查的是位似变换的性质,掌握两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形是解题的关键.

练习册系列答案
相关题目
18.下列关于单项式-$\frac{{4x{y^2}}}{5}$的说法中,正确的是( )
| A. | 系数是$-\frac{4}{5}$,次数是2 | B. | 系数是$\frac{4}{5}$,次数是2 | ||
| C. | 系数是-4,次数是3 | D. | 系数是$-\frac{4}{5}$,次数是3 |
19.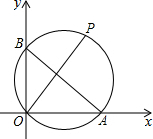 如图,点A的坐标为A(8,0),点B在y轴正半轴上,且AB=10,点P是△AOB外接圆上一点,且∠BOP=45°,则点P的坐标为( )
如图,点A的坐标为A(8,0),点B在y轴正半轴上,且AB=10,点P是△AOB外接圆上一点,且∠BOP=45°,则点P的坐标为( )
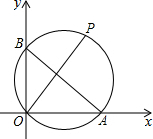 如图,点A的坐标为A(8,0),点B在y轴正半轴上,且AB=10,点P是△AOB外接圆上一点,且∠BOP=45°,则点P的坐标为( )
如图,点A的坐标为A(8,0),点B在y轴正半轴上,且AB=10,点P是△AOB外接圆上一点,且∠BOP=45°,则点P的坐标为( )| A. | (7,7) | B. | (7$\sqrt{2}$,7$\sqrt{2}$) | C. | (5$\sqrt{2}$,5$\sqrt{2}$) | D. | (5,5) |
 如图,已知在正方形ABCD中,点E,G分别在边BC,CD上,且AE=AF.求证:CE=CF.
如图,已知在正方形ABCD中,点E,G分别在边BC,CD上,且AE=AF.求证:CE=CF. 如图所示,AB∥CD,O为∠A、∠C的平分线的交点,OE⊥AC于E,且OE=4,则AB与CD之间的距离等于8.
如图所示,AB∥CD,O为∠A、∠C的平分线的交点,OE⊥AC于E,且OE=4,则AB与CD之间的距离等于8.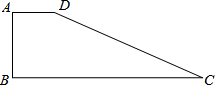 如图在四边形ABCD中,∠A=90°,AD=6,AB=8,BC=26,CD=24.
如图在四边形ABCD中,∠A=90°,AD=6,AB=8,BC=26,CD=24.