题目内容
14.观察下列各式:$\frac{1}{1×2}$=1-$\frac{1}{2}$,$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$,$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$,…(1)求和:$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2009×2010}$
(2)请根据以上的各式的变形方式,对下列各题进行探究变形(不要填最终的结果)
①$\frac{1}{2×4}$=$\frac{1}{2}$($\frac{1}{2}$-$\frac{1}{4}$);②$\frac{1}{4×6}$=$\frac{1}{2}$($\frac{1}{4}$-$\frac{1}{6}$);③$\frac{1}{98×100}$=$\frac{1}{2}$($\frac{1}{98}$-$\frac{1}{100}$);
(2)由你所找到的规律计算:
$\frac{1}{2×4}$+$\frac{1}{4×6}$+$\frac{1}{6×8}$+…+$\frac{1}{98×100}$.
分析 (1)根据题中给出的例子进行计算即可;
(2)根据给出的例子进行探究即可;
(3)根据(2)中的结果进行计算.
解答 解:(1)由题意得,原式=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{2009}$-$\frac{1}{2010}$
=1-$\frac{1}{2010}$
=$\frac{2009}{2010}$;
(2)①$\frac{1}{2×4}$=$\frac{1}{8}$=$\frac{1}{2}$($\frac{1}{2}$-$\frac{1}{4}$);
②$\frac{1}{4×6}$=$\frac{1}{24}$=$\frac{1}{2}$($\frac{1}{4}$-$\frac{1}{6}$);
③$\frac{1}{98×100}$=$\frac{1}{9800}$=$\frac{1}{2}$($\frac{1}{98}$-$\frac{1}{100}$).
故答案为:$\frac{1}{2}$($\frac{1}{2}$-$\frac{1}{4}$),$\frac{1}{2}$($\frac{1}{4}$-$\frac{1}{6}$),$\frac{1}{2}$($\frac{1}{98}$-$\frac{1}{100}$);
(3)由(2)可知,原式=$\frac{1}{2}$($\frac{1}{2}$-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{6}$+$\frac{1}{6}$-$\frac{1}{8}$+…+$\frac{1}{98}$-$\frac{1}{100}$)
=$\frac{1}{2}$($\frac{1}{2}$-$\frac{1}{100}$)
=$\frac{1}{2}$×$\frac{49}{100}$
=$\frac{49}{200}$.
点评 本题考查的是有理数的混合运算,熟知有理数混合运算的法则是解答此题的关键.

 如图,⊙O的弦AB=18,M是AB的中点,且OM=12,则⊙O的半径等于( )
如图,⊙O的弦AB=18,M是AB的中点,且OM=12,则⊙O的半径等于( )| A. | 8 | B. | 2 | C. | 10 | D. | 15 |
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
 如图,在一正方形ABCD中,E为对角线AC上一点,连接EB、ED.
如图,在一正方形ABCD中,E为对角线AC上一点,连接EB、ED. 如图,∠A=∠F,∠C=∠D,判断BD与CE的位置关系,并说明理由.
如图,∠A=∠F,∠C=∠D,判断BD与CE的位置关系,并说明理由.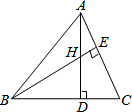 如图,已知AD和BE都是△ABC的高,且AD=BD,AC=4,H是高AD和BE的交点,则线段BH的长度为( )
如图,已知AD和BE都是△ABC的高,且AD=BD,AC=4,H是高AD和BE的交点,则线段BH的长度为( )