题目内容
4.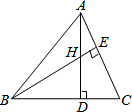 如图,已知AD和BE都是△ABC的高,且AD=BD,AC=4,H是高AD和BE的交点,则线段BH的长度为( )
如图,已知AD和BE都是△ABC的高,且AD=BD,AC=4,H是高AD和BE的交点,则线段BH的长度为( )| A. | 3 | B. | 4 | C. | 3.5 | D. | 5 |
分析 首先根据三角形内角和定理证明∠HBD=∠HAE,然后证明△BDH≌△ADC,根据全等三角形的对应边相等即可求解.
解答 解:∵AD和BE是△ABC的高,
∴直角△BDH和直角△AEH中,∠HBD+∠BHD=90°,∠HAE+∠AHE=90°,
又∵∠BHD=∠AHE,
∴∠HBD=∠HAE,
∴在△BDH和△ADC中,$\left\{\begin{array}{l}{∠HBD=∠HDE}\\{BD=AD}\\{∠BDH=∠ADC}\end{array}\right.$,
∴△BDH≌△ADC,
∴BH=AC=4.
故选B.
点评 本题考查了三角形全等的判定与性质,正确证明△BDH≌△ADC是本题的关键.

练习册系列答案
相关题目
14.多项式x2-2x-1的各项分别是( )
| A. | x2,2x,1 | B. | x2,-2x,1 | C. | -x2,2x,-1 | D. | x2,-2x,-1 |
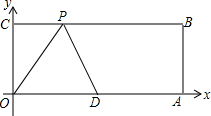 如图,O为坐标原点,四边形OABC为长方形,边OA和OC分别落在x轴和y轴的正半轴上,且A(10,0),C(0,4),点D是OA的中点,点P在线段BC上运动,当△ODP为腰长为5的等腰三角形时,求点P的坐标.
如图,O为坐标原点,四边形OABC为长方形,边OA和OC分别落在x轴和y轴的正半轴上,且A(10,0),C(0,4),点D是OA的中点,点P在线段BC上运动,当△ODP为腰长为5的等腰三角形时,求点P的坐标. 如图中平面展开图折叠成正方体后,相对面上两个数之和为8,则x=6,y=5.
如图中平面展开图折叠成正方体后,相对面上两个数之和为8,则x=6,y=5.