题目内容
2.有长度分别为3cm,4cm,5cm,8cm的四条线段,任取其中三条能组成三角形的概率是$\frac{1}{2}$.分析 根据三角形的三边关系求出共有几种情况,根据概率的求法,找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率.
解答 解:
长度为3cm、4cm、5cm、8cm的四条线段,从中任取三条线段共有3,4,5;4,5,8;3,5,8;3,4,8四种情况,
而能组成三角形的有3、4、5;4、5、8共有2种情况,
所以能组成三角形的概率=$\frac{2}{4}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 此题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.现有3cm,3m,7cm,9cm长的四根木棒,任取其中三根组成一个三角形,那么可以组成的三角形的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.下列有关圆的说法中,不正确的是( )
| A. | 相等的弦所对的优弧和劣弧相等 | |
| B. | 同弧所对的圆周角相等 | |
| C. | 圆是中心对称图形、圆心是它的对称中心 | |
| D. | 在同圆或等圆中,相等的圆心角所对的弦相等,所对的弧也相等 |
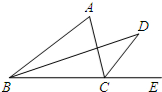 如图,B、C、E三点共线,BD平分∠ABC,CD平分∠ACE,
如图,B、C、E三点共线,BD平分∠ABC,CD平分∠ACE,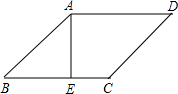 如图,在菱形ABCD中,AE⊥BC于E,EC=2,tanB=$\frac{5}{12}$,求菱形的边长.
如图,在菱形ABCD中,AE⊥BC于E,EC=2,tanB=$\frac{5}{12}$,求菱形的边长. 如图中平面展开图折叠成正方体后,相对面上两个数之和为8,则x=6,y=5.
如图中平面展开图折叠成正方体后,相对面上两个数之和为8,则x=6,y=5.