题目内容
9. 如图,在一正方形ABCD中,E为对角线AC上一点,连接EB、ED.
如图,在一正方形ABCD中,E为对角线AC上一点,连接EB、ED.(1)求证:△BEC≌△DEC;
(2)延长BE交AD于点F,若∠DEB=150°.求∠AFE的度数.
分析 (1)由正方形的性质得出CD=CB,∠DCA=∠BCA,根据SAS即可得出结论;
(2)由全等三角形的对应角相等得出∠DEC=∠BEC=70°,然后根据对顶角相等求出∠AEF,根据正方形的性质求出∠DAC,最后根据三角形的内角和定理即可求出结果.
解答 (1)证明:∵四边形ABCD是正方形,
∴CD=CB,∠DCA=∠BCA,
在△BEC和△DEC中,
$\left\{\begin{array}{l}{CD=CB}\\{∠DCA=∠BCA}\\{CE=CE}\end{array}\right.$,
∴△BEC≌△DEC(SAS);
(2)解:由(1)得△BEC≌△DEC,
∴∠DEC=∠BEC=$\frac{1}{2}$∠DEB=70°,
∴∠AEF=∠BEC=70°,
∵四边形ABCD是正方形,
∴∠DAC=45°,
∴∠AFE=180°-70°-45°=65°.
点评 本题考查了正方形的性质、全等三角形的判定与性质、三角形的内角和定理、对顶角相等等知识;熟练掌握全等三角形的判定与性质、三角形的内角和定理是解题的关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
17.下列有关圆的说法中,不正确的是( )
| A. | 相等的弦所对的优弧和劣弧相等 | |
| B. | 同弧所对的圆周角相等 | |
| C. | 圆是中心对称图形、圆心是它的对称中心 | |
| D. | 在同圆或等圆中,相等的圆心角所对的弦相等,所对的弧也相等 |
18.如果2x3myn+4与-3x9y3n是同类项,那么m、n的值分别为( )
| A. | m=-2,n=3 | B. | m=2,n=3 | C. | m=3,n=2 | D. | m=3,n=2 |
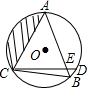 如图,在⊙O中,$\widehat{AD}$=$\widehat{AC}$,弦CD与弦AB交于点E,连接BC,若⊙O的半径长为4cm,∠ACD=60°,求图中阴影部分的面积.
如图,在⊙O中,$\widehat{AD}$=$\widehat{AC}$,弦CD与弦AB交于点E,连接BC,若⊙O的半径长为4cm,∠ACD=60°,求图中阴影部分的面积. 如图,∠1=70°,∠2=130°,直线m平移后得到直线n,则∠3=20°.
如图,∠1=70°,∠2=130°,直线m平移后得到直线n,则∠3=20°.