题目内容
8.计算:(1)解不等式$\frac{x+1}{2}$+$\frac{x-1}{3}$≤1,并把它的解集表示在数轴上;
(2)解不等式组:$\left\{\begin{array}{l}{3x+1<(x+2)}\\{-x≤5x+6}\end{array}\right.$.
分析 (1)根据解不等式的方法可以求得不等式$\frac{x+1}{2}$+$\frac{x-1}{3}$≤1的解集,从而可以在数轴上表示出这个解集;
(2)根据解不等式组的方法可以求得不等式组:$\left\{\begin{array}{l}{3x+1<(x+2)}\\{-x≤5x+6}\end{array}\right.$的解集.
解答 解:(1)$\frac{x+1}{2}$+$\frac{x-1}{3}$≤1
不等式两边同乘以6,得
3(x+1)+2(x-1)≤6
去括号,得
3x+3+2x-2≤6
移项及合并同类项,得
5x≤5
系数化为1,得
x≤1,
故原不等式的解集是x≤1,在数轴上表示出来是,
(2)$\left\{\begin{array}{l}{3x+1<(x+2)}&{①}\\{-x≤5x+6}&{②}\end{array}\right.$
由①,得
x<$\frac{1}{2}$,
由②,得
x≥-1,
由①②得,原不等式组的解集是-1≤x<$\frac{1}{2}$.
点评 本题考查解一元一次不等式、在数轴上表示不等式的解集、解一元一次不等式组,解题的关键是明确解一元一次不等式的方法.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案
相关题目
20.下列图形中,经过折叠不能围成一个正方体的是( )
| A. |  | B. |  | C. |  | D. |  |
18.计算6÷(-2)的结果是( )
| A. | -3 | B. | -$\frac{1}{3}$ | C. | 3 | D. | -12 |
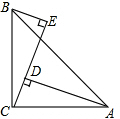 已知:∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE,证明:AD=DE+BE.
已知:∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE,证明:AD=DE+BE.