题目内容
3.解方程组:(1)$\left\{\begin{array}{l}{x-2y=1}\\{3x-5y=8}\end{array}\right.$(用代入消元法解方程组)
(2)$\left\{\begin{array}{l}{3x-2(x+2y)=3}\\{11x+4(x+2y)=45}\end{array}\right.$.
分析 (1)方程组利用代入消元法求出解即可;
(2)方程组整理后,利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{x-2y=1①}\\{3x-5y=8②}\end{array}\right.$,
由①得:x=2y+1③,
把③代入②得:6y+3-5y=8,即y=5,
把y=5代入①得:x=11,
则方程组的解为$\left\{\begin{array}{l}{x=11}\\{y=5}\end{array}\right.$;
(2)方程组整理得:$\left\{\begin{array}{l}{x-4y=3①}\\{15x+8y=45②}\end{array}\right.$,
①×2+②得:17x=51,即x=3,
把x=3代入①得:y=0,
则方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=0}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
相关题目
 已知:∠MAN,求作一个菱形ABCD,使∠MAN为菱形ABCD的一个内角.(尺规作图,不写作法,保留作图痕迹)
已知:∠MAN,求作一个菱形ABCD,使∠MAN为菱形ABCD的一个内角.(尺规作图,不写作法,保留作图痕迹)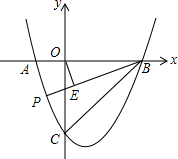 抛物线y=x2-2x-3交x轴于A、B两点(A在B的左侧),交y轴于点C,P是第三象限的抛物线上一点,OE⊥PB于E,连接CE,当∠PEC=45°时,求点P的坐标.
抛物线y=x2-2x-3交x轴于A、B两点(A在B的左侧),交y轴于点C,P是第三象限的抛物线上一点,OE⊥PB于E,连接CE,当∠PEC=45°时,求点P的坐标. 如图所示,A(1,0)、点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为(-3,2).
如图所示,A(1,0)、点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为(-3,2).