Question

19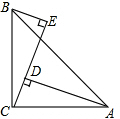．已知：∠ACB=90°，AC=BC，BE⊥CE，AD⊥CE，证明：AD=DE+BE．

Answer 1

分析 根据垂直定义求出∠BEC=∠ACB=∠ADC，根据等式性质求出∠ACD=∠CBE，根据AAS证出△ADC和△CEB全等；推出CD=BE，AD=CE，即可推出答案．

解答 证明：∵∠ACB=90°，BE⊥CE，AD⊥CE，
∴∠BEC=∠ACB=∠ADC=90°，
∴∠ACE+∠BCE=90°，∠BCE+∠CBE=90°，
∴∠ACD=∠CBE，
在△ADC和△CEB中，
$\left\{\begin{array}{l}{∠ADC=∠BEC}&{\;}\\{∠ACD=∠CBE}&{\;}\\{AC=BC}&{\;}\end{array}\right.$，
∴△ADC≌△CEB（AAS）．
∴BE=CD，AD=CE，
∵CE=CD+DE=DE+BE，
∴AD=DE+BE．

点评 本题考查了全等三角形的性质和判定，垂线的定义等知识点的应用，解此题的关键是推出证明△ADC和△CEB全等的三个条件．