题目内容
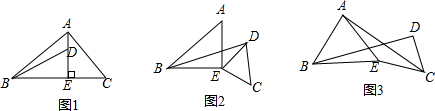
17.如图1,在△ABC中,AE⊥BC于E,AE=BE,D是AE上的一点,且DE=CE,连结BD、CD.(1)判断BD与AC的位置关系和数量关系,并证明;
(2)如图2,若将△DCE绕点E旋转一定的角度后,BD与AC的位置关系和数量关系是否发生变化?并证明;
(3)如图3,将(2)中的等腰直角三角形都换成等边三角形,其他条件不变,求BD与AC夹角的度数.
分析 (1)先判断出∠BED=∠AEC=90°,再判定△DBE≌△CAE,再判断∠ADF+∠CAE=90°,
(2)先判断出△BED≌△AEC,再得到∠BFC=∠ACD+∠CDE+∠BDE=∠ACD+∠CDE+∠ACE=90°,
(3)先判断出∠BED=∠AEC,再判断出△BED≌△AEC,最后计算即可.
解答 解:(1)BD与AC的位置关系是:BD⊥AC,数量关系是BD=AC.
理由如下:
延长BD交AC于点F.
∵AE⊥BC于E,
∴∠BED=∠AEC=90°.
∵AE=BE,DE=CE,
∴△DBE≌△CAE,
∴BD=AC,∠DBE=∠CAE,∠BDE=∠ACE.
∵∠BDE=∠ADF,
∴∠ADF=∠ACE.
∵∠ACE+∠CAE=90°,
∴∠ADF+∠CAE=90°,
∴BD⊥AC.
(2)①∵∠AEB=∠DEC=90°,
∴∠AEB+∠AED=∠DEC+∠AED,
即∠BED=∠AEC.
∵AE=BE,DE=CE,
∴△BED≌△AEC,
∴BD=AC,∠BDE=∠ACE,∠DBE=∠CAE.
∵∠BFC=∠ACD+∠CDE+∠BDE=∠ACD+∠CDE+∠ACE=90°,
∴BD⊥AC.
②BD与AC的数量关系是:BD=AC.
∵△ABE和△DCE是等边三角形,
∴∠AEB=∠ABE=60°,AE=BE,
∠DEC=∠DCE=60°,DE=CE,
∴∠AEB+∠AED=∠DEC+∠AED,
∴∠BED=∠AEC,
∴△BED≌△AEC.
∴BD=AC.
(3)∵△ABE和△DEC是等边三角形,
∴AE=BE,DE=EC,∠EDC=∠DCE=60°,∠BEA=∠DEC=60°,
∴∠BEA+∠AED=∠DEC+∠AED,
∴∠BED=∠AEC,
在△BED和△AEC中,
$\left\{\begin{array}{l}{BE=AE}\\{∠BED=∠AEC}\\{DE=EC}\end{array}\right.$
∴△BED≌△AEC,
∴∠BED=∠ACE,
∴∠DFC=180°-(∠BDE+∠EDC+∠DCF)=60°
∴BD与AC的夹角度数为60°或120°.
点评 此题是几何变换综合题,主要考查了全等三角形的判定和性质,等边三角形的性质,判断垂直的方法,解本题的关键是判断△DBE≌△CAE.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. |  | B. |  | C. |  | D. |  |
| A. | 1 | B. | 2 | C. | ±1 | D. | ±2 |

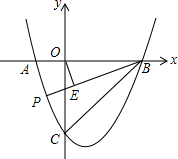 抛物线y=x2-2x-3交x轴于A、B两点(A在B的左侧),交y轴于点C,P是第三象限的抛物线上一点,OE⊥PB于E,连接CE,当∠PEC=45°时,求点P的坐标.
抛物线y=x2-2x-3交x轴于A、B两点(A在B的左侧),交y轴于点C,P是第三象限的抛物线上一点,OE⊥PB于E,连接CE,当∠PEC=45°时,求点P的坐标.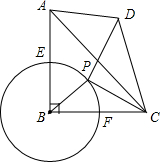 如图,在等腰直角三角形ABC中,∠ABC=90°,AB=BC=4,⊙B与AB、BC交于E、F,点P是弧EF上的一个动点,连接PC,线段PC绕P点逆时针旋转90°到PD,连接CD,AD.
如图,在等腰直角三角形ABC中,∠ABC=90°,AB=BC=4,⊙B与AB、BC交于E、F,点P是弧EF上的一个动点,连接PC,线段PC绕P点逆时针旋转90°到PD,连接CD,AD.