题目内容
4. 如图,AB为⊙O的直径,E为⊙O上一点,∠EAB的平分线AC交⊙O于C点,过C点作CD⊥AE交AE的延长线于D点,直线CD与射线AB交于P点.
如图,AB为⊙O的直径,E为⊙O上一点,∠EAB的平分线AC交⊙O于C点,过C点作CD⊥AE交AE的延长线于D点,直线CD与射线AB交于P点.(1)求证:DC为⊙O切线;
(2)若DC=1,AC=$\sqrt{5}$,求⊙O的半径长.
分析 (1)连接OC,根据角平分线的定义、等腰三角形的性质证明OC∥AD,得到∠OCP=∠D=90°,根据切线的判定定理证明;
(2)连接BC,根据勾股定理求出AD,根据相似三角形的性质计算即可.
解答 (1)证明: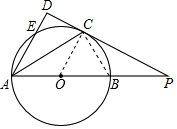 连接OC,
连接OC,
∵AC是∠EAB的平分线,
∴∠DAC=∠OAC,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠DAC=∠OCA,
∴OC∥AD,
∴∠OCP=∠D=90°,
∴DC为⊙O切线;
(2)解:连接BC,
∵∠D=90°,DC=1,AC=$\sqrt{5}$,
∴AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=2,
∵∠OAC=∠OCA,∠ACB=∠D,
∴△ADC∽△ACB,
∴$\frac{AD}{AC}$=$\frac{AC}{AB}$,即AC2=AD•AB,
则AB=$\frac{A{C}^{2}}{AD}$=$\frac{5}{2}$,
∴⊙O的半径长为$\frac{5}{4}$.
点评 本题考查的是切线的判定、相似三角形的判定和性质、勾股定理的应用,掌握经过半径的外端且垂直于这条半径的直线是圆的切线是解题的关键.

练习册系列答案
相关题目
9.抛物线y=ax2+bx+c上,部分点的横、纵坐标x、y的对应值如下表:
(1)根据上表填空;
①方程ax2+bx+c=0的两个根分别是x1=-2和x2=1.
②抛物线经过点(-3,8);
③在对称轴左侧,y随x增大而减小;
(2)求抛物线y=ax2+bx+c的解析式.
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | -4 | -4 | 0 | 8 |
①方程ax2+bx+c=0的两个根分别是x1=-2和x2=1.
②抛物线经过点(-3,8);
③在对称轴左侧,y随x增大而减小;
(2)求抛物线y=ax2+bx+c的解析式.
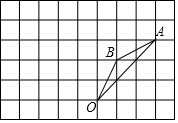 如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A,B的坐标分别是A(3,3)、B(1,2),△AOB绕点O逆时针旋转90°后得到△A1OB1.
如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A,B的坐标分别是A(3,3)、B(1,2),△AOB绕点O逆时针旋转90°后得到△A1OB1.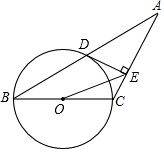 如图,已知等腰三角形ABC的底角为30°,以腰BC为直径的⊙O与底边AB交于点D,过点D作DE⊥AC,垂足为E.
如图,已知等腰三角形ABC的底角为30°,以腰BC为直径的⊙O与底边AB交于点D,过点D作DE⊥AC,垂足为E.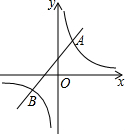 如图,已知反比例函数y1=$\frac{k}{x}$的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).
如图,已知反比例函数y1=$\frac{k}{x}$的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).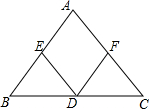 如图,D、E、F分别是BC、AB、AC的点,DF∥AB,DE∥AC,∠FDE=70°,求∠A的度数.
如图,D、E、F分别是BC、AB、AC的点,DF∥AB,DE∥AC,∠FDE=70°,求∠A的度数.