题目内容
10.甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过100元后,超出100元的部分按90%收费;在乙商场累计购物超过50元后,超出50元的部分按95%收费.(1)如果不使用优惠方案,某人购买2件A商品和1件B商品应付30元,购买1件A商品和2件B商品应付50元,如果使用优惠方案购买3件A商品和5件B商品,应到哪家商场更省钱?
(2)若使用优惠方案前,顾客购物应付x元,请根据x的取值,讨论顾客到哪家商场购物花费少?
分析 (1)求得A、B商品的价格,然后分别求得甲、乙商场优惠方案购买3件A商品和5件B商品的费用,进行比较即可;
(2)根据题意,分情况讨论,选择花费较少的商场.
解答 解:(1)设A商品每件x元,B商品每件y元,根据题意得
$\left\{\begin{array}{l}{2x+y=30}\\{x+2y=50}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=\frac{10}{3}}\\{y=\frac{70}{3}}\end{array}\right.$.
甲:100+(3×$\frac{10}{3}$+5×$\frac{70}{3}$-100)×90%=124元,
乙:50+(3×$\frac{10}{3}$+5×$\frac{70}{3}$-50)×95%=122.8元,
因为甲>乙,所以到乙商场省钱;
(2)设费用为W,根据题意,
W甲=100+(x-100)×90%=0.9x+10,
W乙=50+(x-50)×95%=0.95x+2.5;
①0.9x+10=0.95x+2.5,
解得:x=150.
∴当x=150时,顾客在甲、乙两商场的实际花费相同,
②0.9x+10<0.95x+2.5,
解得:x>150.
则当顾客累计购物大于150时,选择甲商场实际花费少;
③0.9x+10>0.95x+2.5,
解得:x<150.
当顾客累计购物超过100元而不到150元时,在乙商场实际花费少.
点评 此题主要考查了一元一次不等式的应用和一元一次方程的应用,解决问题的关键是读懂题意,依题意列出相关的式子进行求解.本题涉及方案选择时应与方程或不等式联系起来.

练习册系列答案
相关题目
20.若分式$\frac{{x}^{2}+1}{2-x}$的值是正值,则x的取值范围是( )
| A. | x>2 | B. | x≥2 | C. | x<2 | D. | x≤2 |



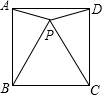 如图,等边△BCP在正方形ABCD内,则∠APD=150度.
如图,等边△BCP在正方形ABCD内,则∠APD=150度. 已知:如图,在菱形ABCD中,E是AB上一点,线段DE与菱形对角线AC交于点F,点O是AC的中点,EO的延长线交边DC于点G
已知:如图,在菱形ABCD中,E是AB上一点,线段DE与菱形对角线AC交于点F,点O是AC的中点,EO的延长线交边DC于点G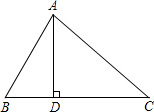 已知:如图,在△ABC中,AD⊥BC于D,∠B=60°,∠C=45°.
已知:如图,在△ABC中,AD⊥BC于D,∠B=60°,∠C=45°.