Question

5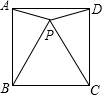．如图，等边△BCP在正方形ABCD内，则∠APD=150度．

Answer 1

分析 由正方形的性质和等边三角形的性质得出AB=BP=CP=CD，∠ABP=∠DCP=30°，由三角形内角和定理求出∠BAP=∠BPA=∠CDP=∠CPD=75°，再求出∠PAD=∠PDA=15°，然后由三角形内角和定理求出∠APD即可．

解答 解：∵四边形ABCD是正方形，
∴AB=BC=CD=DA，∠BAD=∠ABC=∠BCD=∠CDA=90°，
∵△BCP是等边三角形，
∴BP=CP=BC，∠PBC=∠BCP=∠BPC=60°，
∴AB=BP=CP=CD，∠ABP=∠DCP=90°-60°=30°，
∴∠BAP=∠BPA=∠CDP=∠CPD=$\frac{1}{2}$（180°-30°）=75°，
∴∠PAD=∠PDA=90°-75°=15°，
∴∠APD=180°-15°-15°=150°；
故答案为：150．

点评 本题考查了正方形的性质、等边三角形的性质、三角形内角和定理、等腰三角形的性质；熟练掌握正方形和等边三角形的性质，并能进行推理计算是解决问题的关键．