题目内容
2.甲、乙两人轮流做下面的游戏:掷一枚均匀的骰子(每上面分别标有1,2,3,4,5,6这六个数字),如果朝上的数字大于3,则甲获胜,如果朝上的数字小于3,则乙获胜,你认为获胜的可能性比较大的是甲.分析 首先根据可能性大小的求法,分别求出两人获胜的可能性各是多少;然后比较大小,判断出谁获胜的可能性比较大即可.
解答 解:∵1,2,3,4,5,6这六个数字中大于3的数字有3个:4、5、6,
∴P(甲获胜)=$\frac{3}{6}=\frac{1}{2}$;
∵1,2,3,4,5,6这六个数字中小于3的数字有2个:1、2,
∴P(乙获胜)=$\frac{2}{6}=\frac{1}{3}$;
∵$\frac{1}{2}>\frac{1}{3}$,
∴获胜的可能性比较大的是甲.
故答案为:甲.
点评 此题主要考查了可能性的大小,要熟练掌握,解答此类问题的关键是要明确:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.

练习册系列答案
相关题目
14.下列二次根式中,属于最简二次根式的是( )
| A. | $\sqrt{25a}$ | B. | $\sqrt{0.5}$ | C. | $\sqrt{\frac{a}{2}}$ | D. | $\sqrt{{a}^{2}{+b}^{2}}$ |
11.在同一平面内,两条直线的位置关系是( )
| A. | 平行 | B. | 相交 | C. | 垂直 | D. | 平行或相交 |
 如图,l1∥l2,A,B,C是l1上的点,D,E,F是l2上的点,∠1=∠2,BD平分∠ABE,FB平分∠CFE.
如图,l1∥l2,A,B,C是l1上的点,D,E,F是l2上的点,∠1=∠2,BD平分∠ABE,FB平分∠CFE. 如图,正方形ABCD中,E为对角线BD上一点,且BC=BE,则∠BEC=67.5°.
如图,正方形ABCD中,E为对角线BD上一点,且BC=BE,则∠BEC=67.5°.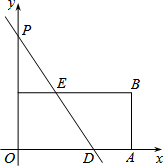 如图,在平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(12,0)、(12,6),直线y=-$\frac{3}{2}$x+b与y轴交于点P,与边OA交于点D,与边BC交于点E.
如图,在平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(12,0)、(12,6),直线y=-$\frac{3}{2}$x+b与y轴交于点P,与边OA交于点D,与边BC交于点E.