题目内容
2013年我国多地出现雾霾天气,某企业抓住商机准备生产空气净化设备,该企业决定从以下两个投资方案中选择一个进行投资生产,方案一:生产甲产品,每件产品成本为a元(a为常数,且40<a<100),每件产品销售价为120元,每年最多可生产125万件;方案二:生产乙产品,每件产品成本价为80元,每件产品销售价为180元,每年可生产120万件,另外,年销售x万件乙产品时需上交0.5x2万元的特别关税,在不考虑其它因素的情况下:
(1)分别写出该企业两个投资方案的年利润y1(万元)、y2(万元)与相应生产件数x(万件)(x为正整数)之间的函数关系式,并指出自变量的取值范围;
(2)分别求出这两个投资方案的最大年利润;
(3)如果你是企业决策者,为了获得最大收益,你会选择哪个投资方案?
(1)分别写出该企业两个投资方案的年利润y1(万元)、y2(万元)与相应生产件数x(万件)(x为正整数)之间的函数关系式,并指出自变量的取值范围;
(2)分别求出这两个投资方案的最大年利润;
(3)如果你是企业决策者,为了获得最大收益,你会选择哪个投资方案?
考点:二次函数的应用
专题:
分析:(1)根据题意直接得出y1与y2与x的函数关系式即可;
(2)根据a的取值范围可知y1随x的增大而增大,可求出y1的最大值.又因为-0.5<0,可求出y2的最大值;
(3)第三问要分两种情况决定选择方案一还是方案二.当2000-200a>500以及2000-200a<500.
(2)根据a的取值范围可知y1随x的增大而增大,可求出y1的最大值.又因为-0.5<0,可求出y2的最大值;
(3)第三问要分两种情况决定选择方案一还是方案二.当2000-200a>500以及2000-200a<500.
解答:解:(1)由题意得:
y1=(120-a)x(1≤x≤125,x为正整数),
y2=100x-0.5x2(1≤x≤120,x为正整数);
(2)①∵40<a<100,∴120-a>0,
即y1随x的增大而增大,
∴当x=125时,y1最大值=(120-a)×125=15000-125a(万元)
②y2=-0.5(x-100)2+5000,
∵a=-0.5<0,
∴x=100时,y2最大值=5000(万元);
(3)∵由15000-125a>5000,
∴a<80,
∴当40<a<80时,选择方案一;
由15000-125a=5000,得a=80,
∴当a=80时,选择方案一或方案二均可;
由15000-125a<5000,得a>80,
∴当80<a<100时,选择方案二.
y1=(120-a)x(1≤x≤125,x为正整数),
y2=100x-0.5x2(1≤x≤120,x为正整数);
(2)①∵40<a<100,∴120-a>0,
即y1随x的增大而增大,
∴当x=125时,y1最大值=(120-a)×125=15000-125a(万元)
②y2=-0.5(x-100)2+5000,
∵a=-0.5<0,
∴x=100时,y2最大值=5000(万元);
(3)∵由15000-125a>5000,
∴a<80,
∴当40<a<80时,选择方案一;
由15000-125a=5000,得a=80,
∴当a=80时,选择方案一或方案二均可;
由15000-125a<5000,得a>80,
∴当80<a<100时,选择方案二.
点评:此题属于一次函数和二次函数的综合的应用题,考查数列模型的构建,考查利用数学知识解决实际问题,解题的构建是确定数列模型.

练习册系列答案
相关题目
 反比例函数y=
反比例函数y=| k |
| x |
| k |
| x |
| BC |
| AO |
A、
| ||||
B、2-
| ||||
C、
| ||||
D、
|
若∠1和∠2互为余角,∠1和∠3互为补角,∠2和∠3的和等于周角的三分之一,那么∠1、∠2、∠3的度数分别为( )
| A、75°、15°、105° |
| B、60°、30°、120° |
| C、50°、40°、130° |
| D、70°、20°、110° |
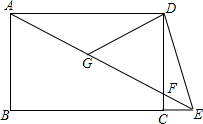 如图,点E是矩形ABCD的边BC延长线上一点,连接AE,交CD于点F,G是AF的中点,再连接DG、DE,且DE=DG.
如图,点E是矩形ABCD的边BC延长线上一点,连接AE,交CD于点F,G是AF的中点,再连接DG、DE,且DE=DG.