题目内容
设m＞n＞0，m2+n2=4mn，求
的值．
| m2-n2 |
| mn |
考点：代数式求值
专题：
分析：由m2+n2=（m+n）2-2mn求得m+n=
．然后根据代数式的变形得到m-n=
；最后对所求的代数式进行变形，然后通过代入法进行求值．
| 6mn |
| 2mn |
解答：解：∵m2+n2=4mn，
∴（m+n）2=m2+n2+2mn=6mn，
∵m＞n＞0，
∴m+n=
．
∴（m-n）2=（m+n）2-4mn=6mn-4mn=2mn，
∴m-n=
，
∴
=
=
=2
．
∴（m+n）2=m2+n2+2mn=6mn，
∵m＞n＞0，
∴m+n=
| 6mn |
∴（m-n）2=（m+n）2-4mn=6mn-4mn=2mn，
∴m-n=
| 2mn |
∴
| m2-n2 |
| mn |
| (m+n)(m-n) |
| mn |
| ||||
| mn |
| 3 |
点评：本题考查了代数式求值．此题对代数式进行变形时，需要熟记完全平方公式和平方差公式．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
一只口袋中装有3个白球和9个黑球，这些球只有颜色不同，随机从口袋中摸出1个球，摸出白球的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
直角三角形两直角边长分别为
和1，那么它的外接圆的直径是（ ）
| 3 |
| A、1 | B、2 | C、3 | D、4 |
如果方程2x+8=-6与关于x的方程2x-3a=-5的解相同，则a的值为（ ）
| A、13 | B、3 | C、-3 | D、8 |
|
A、±
| ||
B、±
| ||
C、
| ||
D、
|
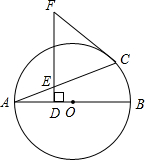如图，AB是⊙O的直径，DF⊥AB于点D，交弦AC于点E，FC=FE．