��Ŀ����
12����֪��ͼ����ƽ��ֱ������ϵ�У�O������ԭ�㣬ֱ��l��y=kx-1����������ֱ���A��B����OB=2OA����P�ǵ�һ������ֱ��l�ϵĵ㣬����P�ֱ�����������Ĵ��ߣ�����ֱ�ΪC��D����1�����A�����꼰k��ֵ��
��2�����P�ĺ�����Ϊx���ı���OCPD�����Ϊy���Խ���y����x�ĺ�����ϵʽ����д������������
��3�����ı���OCPD�����Ϊ1����Q��x���������ϵĵ㣬�ҡ�POQ�ǵ��������Σ����Q�����꣮

���� ��1������ֱ��l�Ľ���ʽΪy=kx-1�����A��$\frac{1}{k}$��0����B��0��-1��������OB=2OA�����k��ֵ����A�����ꣻ
��2�����ݵ�P�ǵ�һ������ֱ��l�ϵĵ㣬��P�ĺ�����Ϊx���ɵ�P��x��2x-1����x��$\frac{1}{2}$���ٸ��ݾ��������ʽ������⣻
��3�������ı���OCPD�����Ϊ1�����P������Ϊ��1��1�������������ľ��빫ʽ���OP=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$���ٷ���������������ۣ���OQ=OP=$\sqrt{2}$����PO=PQ����QO=QP��
��� �⣺��1����y=kx-1��
�൱y=0ʱ��kx-1=0��x=$\frac{1}{k}$��
��A��$\frac{1}{k}$��0����OA=$\frac{1}{k}$��
��x=0ʱ��y=-1��
��B��0��-1����OB=1��
��OB=2OA��
��2��$\frac{1}{k}$=1��
��k=2��
��A��$\frac{1}{2}$��0����
��2����ֱ��l��y=2x-1����P�ǵ�һ������ֱ��l�ϵĵ㣬��P�ĺ�����Ϊx��
��P��x��2x-1����x��$\frac{1}{2}$��
��OC=x��CP=2x-1��
��y=OC•CP=x��2x-1��=2x2-x��
��y=2x2-x��x��$\frac{1}{2}$���� ��3�����ı���OCPD�����Ϊ1��
��3�����ı���OCPD�����Ϊ1��
��2x2-x=1��
��x1=1��x2=-$\frac{1}{2}$������������ȥ����
��P��1��1����OP=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$��
��ͼ������Q��x���������ϵĵ㣬�ҡ�POQ�ǵ���������ʱ�������������
�����OQ=OP=$\sqrt{2}$����ôQ1��$\sqrt{2}$��0����
�����PO=PQ����ôP���߶�OQ�Ĵ�ֱƽ�����ϣ�Q2��2��0����
�����QO=QP����ôQ���߶�OP�Ĵ�ֱƽ�����ϣ�
��P��1��1����
��ֱ��OP�Ľ���ʽΪy=x���߶�OP���е�����Ϊ��$\frac{1}{2}$��$\frac{1}{2}$����
���߶�OP�Ĵ�ֱƽ���ߵĽ���ʽΪy=-x+b��
����$\frac{1}{2}$��$\frac{1}{2}$�����룬��$\frac{1}{2}$=-$\frac{1}{2}$+b�����b=1��
���߶�OP�Ĵ�ֱƽ���ߵĽ���ʽΪy=-x+1��
��y=0ʱ��-x+1=0�����x=1��
��Q3��1��0����
���������������Q������ΪQ1��$\sqrt{2}$��0����Q2��2��0����Q3��1��0����
���� ������һ�κ����ۺ��⣬�����漰�����ô���ϵ������ֱ�ߵĽ���ʽ��һ�κ���ͼ���ϵ���������������ε�����������ľ��빫ʽ�����ഹֱ����ֱ��б��֮��Ϊ-1�����ʣ����������ε����ʵ�֪ʶ���ۺ��Խ�ǿ���Ѷ����У����÷��������Լ����ν���ǽ���Ĺؼ���

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�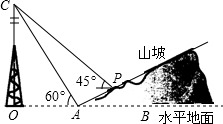 ��ͼ��ʾ��ij����ɽ���½�A����õ��������C������Ϊ60�㣬��ɽ�������ߵ�P���ٲ��C������Ϊ45�㣬��֪OA=200�ף�ɽ���¶�Ϊ$\frac{1}{3}$����tan��PAB=$\frac{1}{3}$������O��A��B��ͬһ��ֱ���ϣ��������OC�ĸ߶��Լ��������ڵ�λ�õ�P�Ĵ�ֱ�߶ȣ����������ĸ߶Ⱥ��Բ��ƣ�����������ţ�
��ͼ��ʾ��ij����ɽ���½�A����õ��������C������Ϊ60�㣬��ɽ�������ߵ�P���ٲ��C������Ϊ45�㣬��֪OA=200�ף�ɽ���¶�Ϊ$\frac{1}{3}$����tan��PAB=$\frac{1}{3}$������O��A��B��ͬһ��ֱ���ϣ��������OC�ĸ߶��Լ��������ڵ�λ�õ�P�Ĵ�ֱ�߶ȣ����������ĸ߶Ⱥ��Բ��ƣ�����������ţ� ��ͼ�����ı���ABCD�У�AD��BC����B=90��AB=8cm��AD=24cm��BC=26cm����P�ӵ�A��������1cm/s���ٶ����D�˶�����Q�ӵ�Cͬʱ��������3cm/s���ٶ����B�˶����涨����һ�����㵽��˵�ʱ����һ������Ҳ��ֹ֮ͣ�˶������˶���ʼ��
��ͼ�����ı���ABCD�У�AD��BC����B=90��AB=8cm��AD=24cm��BC=26cm����P�ӵ�A��������1cm/s���ٶ����D�˶�����Q�ӵ�Cͬʱ��������3cm/s���ٶ����B�˶����涨����һ�����㵽��˵�ʱ����һ������Ҳ��ֹ֮ͣ�˶������˶���ʼ��