题目内容
18.若关于x的多项式ax2-abx+b与bx2+abx+2a的和是一个单项式,且ab≠0,则$\frac{a}{b}$的值为-1或-$\frac{1}{2}$.分析 根据关于x的多项式ax2-abx+b与bx2+abx+2a的和是一个单项式,且ab≠0,可求出a和b之间的关系,然后根据a和b之间的关系进行求解即可.
解答 解:∵关于x的多项式ax2-abx+b与bx2+abx+2a的和是一个单项式,且ab≠0,
∴当a=-b时,
ax2-abx+b+bx2+abx+2a
=-bx2+b2x+b+bx2-b2x+2b
=3b,
∵3b为单项式,
∴a=-b符合题意,
∴$\frac{a}{b}$=-1;
当b=-2a,即a=-$\frac{1}{2}$b时,
ax2-abx+b+bx2+abx+2a
=-$\frac{1}{2}$bx2+$\frac{1}{2}$b2x+b+bx2-$\frac{1}{2}$b2x-b
=$\frac{1}{2}$bx2.
∵$\frac{1}{2}$bx2为单项式,
∴a=-$\frac{1}{2}$b符合题意,
∴$\frac{a}{b}$=-$\frac{1}{2}$.
故答案为:-1或-$\frac{1}{2}$.
点评 本题考查了整式的加减,解答本题的关键在于根据关于x的多项式ax2-abx+b与bx2+abx+2a的和是一个单项式,且ab≠0,求出a和b之间的关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.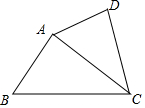 如图,在四边形ABCD中,如果∠ADC=∠BAC,那么下列条件中不能判定△ADC和△BAC相似的是( )
如图,在四边形ABCD中,如果∠ADC=∠BAC,那么下列条件中不能判定△ADC和△BAC相似的是( )
 如图,在四边形ABCD中,如果∠ADC=∠BAC,那么下列条件中不能判定△ADC和△BAC相似的是( )
如图,在四边形ABCD中,如果∠ADC=∠BAC,那么下列条件中不能判定△ADC和△BAC相似的是( )| A. | ∠DAC=∠ABC | B. | AC是∠BCD的平分线 | ||
| C. | AC2=BC•CD | D. | $\frac{AD}{AB}$=$\frac{DC}{AC}$ |
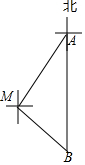 如图,一艘渔船位于小岛M的北偏东30°方向,距离小岛180海里的A处,渔船从A处沿正南方向航行一段距离后,到达位于小岛东南方向的B处
如图,一艘渔船位于小岛M的北偏东30°方向,距离小岛180海里的A处,渔船从A处沿正南方向航行一段距离后,到达位于小岛东南方向的B处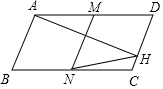 如图,在平行四边形ABCD中,AD=2AB,AH⊥CD于H,M为AD的中点,MN∥AB,连接NH,如果∠D=68°,则∠CHN=56°.
如图,在平行四边形ABCD中,AD=2AB,AH⊥CD于H,M为AD的中点,MN∥AB,连接NH,如果∠D=68°,则∠CHN=56°.