题目内容
6.若抛物线y=x2+(m2+m-6)x+(m+3)的顶点在y轴的正半轴上,则m的取值是( )| A. | 2 | B. | -2 | C. | 3 | D. | -3 |
分析 根据抛物线y=x2+(m2+m-6)x+(m+3)的顶点在y轴的正半轴上,可知顶点的横坐标为0,纵坐标大于0,由此可得m2+m-6=0,m+3>0,解方程即可.
解答 解:∵抛物线的顶点坐标在y轴的正半轴上,
∴顶点的横坐标为0,纵坐标大于0,
即m2+m-6=0,m+3>0,
解得m=2,
故选A.
点评 本题主要考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-$\frac{b}{2a}$$\frac{4ac-{b}^{2}}{4a}$),对称轴直线x=-$\frac{b}{2a}$,比较简单.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
15.若A和B都是4次多项式,则2A+3B一定是( )
| A. | 8次多项式 | B. | 4次多项式 | ||
| C. | 次数不高于4次的整式 | D. | 次数不低于4的整式 |
 如图,AB⊥BD,EF⊥BD,CD⊥BD,且AB:EF:CD=3:5:8 求AE:EC的值.
如图,AB⊥BD,EF⊥BD,CD⊥BD,且AB:EF:CD=3:5:8 求AE:EC的值.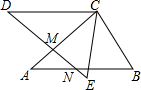 如图,AB=DE,AC=DC,BC=EC,DE与AC、AB分别交于点M、N,CE与AB交于点H,且∠A=∠BCE=40°,∠B=60°
如图,AB=DE,AC=DC,BC=EC,DE与AC、AB分别交于点M、N,CE与AB交于点H,且∠A=∠BCE=40°,∠B=60°