题目内容
19. 如图,在Rt△ABC中∠C=90°,点P、Q同时由A、B两点出发分别沿AC、BC方向向C点匀速运动,其速度为2m/s,几秒后△PCQ的面积是△ABC面积的一半( )
如图,在Rt△ABC中∠C=90°,点P、Q同时由A、B两点出发分别沿AC、BC方向向C点匀速运动,其速度为2m/s,几秒后△PCQ的面积是△ABC面积的一半( )| A. | 1.5 | B. | 9 | C. | 1.5或9 | D. | 10 |
分析 根据题意∠C=90°,可以得出△ABC面积和△PCQ的面积,设出t秒后满足要求,则根据△PCQ的面积是△ABC面积的一半列出等量关系求出t的值即可.
解答 解:设t秒后△PCQ的面积是△ABC面积的一半,则可得此时PC=AC-AP=12-2t,CQ=BC-BQ=9-2t,
∴△ABC面积为$\frac{1}{2}$×AC×BC=$\frac{1}{2}$×12×9=54,△PCQ的面积为$\frac{1}{2}$×PC×CQ=$\frac{1}{2}$(12-2t)(9-2t),
∵△PCQ的面积是△ABC面积的一半,
∴$\frac{1}{2}$(12-2t)(9-2t)=$\frac{1}{2}$×54,
解得t1=1.5,t2=9(不合题意舍去),
即1.5秒后△PCQ的面积是△ABC面积的一半.
故选A.
点评 本题考查了一元二次方程的应用,找到等量关系式,列出方程求解即可.要注意结合图形找到等量关系.

练习册系列答案
相关题目
9.现定义运算“△”,对于任意有理数a、b,都有a△b=a2-ab+b,例如:3△5=32-3×5+5=11,由此算出(x-1)△(2+x)等于( )
| A. | 2x-5 | B. | 2x-3 | C. | -2x+5 | D. | -2x+3 |
7.某商品的标价为800元,4折销售仍可赚60元,则该商品的进价为( )
| A. | 92元 | B. | 260元 | C. | 320元 | D. | 740元 |
14.在下列说法中是错误的是( )
| A. | 在△ABC中,若∠A:∠B:∠C=5:2:3,则△ABC为直角三角形 | |
| B. | 在△ABC中,∠C=∠A-∠B,则△ABC为直角三角形 | |
| C. | 在△ABC中,若a=$\frac{3}{5}$c,b=$\frac{4}{5}$c,则△ABC为直角三角形 | |
| D. | 在△ABC中,若a:b:c=2:2:4,则△ABC为直角三角形 |
4. 如图,∠BCD=150°,则∠A+∠B+∠D的度数为( )
如图,∠BCD=150°,则∠A+∠B+∠D的度数为( )
 如图,∠BCD=150°,则∠A+∠B+∠D的度数为( )
如图,∠BCD=150°,则∠A+∠B+∠D的度数为( )| A. | 110° | B. | 120° | C. | 130° | D. | 150° |
11.设n为正整数,且6<$\sqrt{n}$<7,则n可能为( )
| A. | 25 | B. | 28 | C. | 43 | D. | 58 |
8.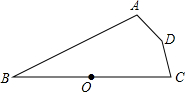 如图,O是线段BC的中点,A、D、C到O点的距离相等,若∠ABC=30°,则∠ADC的度数是( )
如图,O是线段BC的中点,A、D、C到O点的距离相等,若∠ABC=30°,则∠ADC的度数是( )
 如图,O是线段BC的中点,A、D、C到O点的距离相等,若∠ABC=30°,则∠ADC的度数是( )
如图,O是线段BC的中点,A、D、C到O点的距离相等,若∠ABC=30°,则∠ADC的度数是( )| A. | 150° | B. | 120° | C. | 60° | D. | 30° |

 根据如图所示的程序计算函数值,若输入的x的值为$\frac{5}{2}$,则输出的y的值为$\frac{2}{5}$.
根据如图所示的程序计算函数值,若输入的x的值为$\frac{5}{2}$,则输出的y的值为$\frac{2}{5}$.