题目内容
 正方形ABCD中,E是BC延长线上的点,BF⊥DE于F,连接AF,探究线段AF、BF、DF的数量关系.
正方形ABCD中,E是BC延长线上的点,BF⊥DE于F,连接AF,探究线段AF、BF、DF的数量关系.考点:正方形的性质
专题:综合题
分析:根据∠BFD=90°=∠BCD得到A、B、C、F、D五点共圆,然后即可得到AB2=AF2+BF2-2AF•BF•cos45°,AD2=AF2+DF2-2AF•DF•cos45°,最后由这两个关系式即可得到结论.
解答:解:∵∠BFD=90°=∠BCD,
∴A、B、C、F、D五点共圆,
∴∠AFB=∠ACB=45°=∠AFD,
∴AB2=AF2+BF2-2AF•BF•cos45°,
AD2=AF2+DF2-2AF•DF•cos45°,
BF2-
AF•BF=DF2-
AF•DF,
BF2-DF2=(BF+DF)(BF-DF)=
AF(BF-DF),
∴BF+DF=
AF.
∴A、B、C、F、D五点共圆,
∴∠AFB=∠ACB=45°=∠AFD,
∴AB2=AF2+BF2-2AF•BF•cos45°,
AD2=AF2+DF2-2AF•DF•cos45°,
BF2-
| 2 |
| 2 |
BF2-DF2=(BF+DF)(BF-DF)=
| 2 |
∴BF+DF=
| 2 |
点评:该题目考查了正方形的性质、四点共圆,关键是得到点A、B、C、F、D五点共圆.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
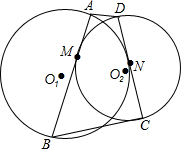 圆O1过梯形ABCD的两顶点A、B,并切腰CD于点N;圆O2过点C、D并切腰AB于点M.求证:AM•MB=CN•ND.
圆O1过梯形ABCD的两顶点A、B,并切腰CD于点N;圆O2过点C、D并切腰AB于点M.求证:AM•MB=CN•ND. 已知四边形ABCD中,AB∥CD,AC=CD,AD=OD,∠BCA=15°.求证:△CBD为等腰直角三角形.
已知四边形ABCD中,AB∥CD,AC=CD,AD=OD,∠BCA=15°.求证:△CBD为等腰直角三角形. 观察如图所示的直四棱柱.
观察如图所示的直四棱柱. 如图,在⊙O的内接四边形ABCD中,∠BAD=60°,∠ACB=70°.求∠BCD和∠ABD的度数.
如图,在⊙O的内接四边形ABCD中,∠BAD=60°,∠ACB=70°.求∠BCD和∠ABD的度数.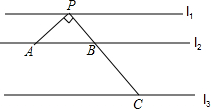 如图,直线l1∥l2∥l3,l1与l2之间的距离为1,l2与l3之间的距离为2,点P在l1上,点A在l2上,点C在l3上,PC交l2于点B,PA⊥PC.
如图,直线l1∥l2∥l3,l1与l2之间的距离为1,l2与l3之间的距离为2,点P在l1上,点A在l2上,点C在l3上,PC交l2于点B,PA⊥PC.