题目内容
19．
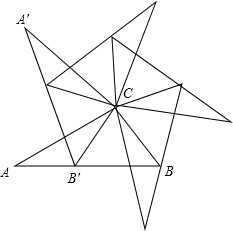如图，在△ABC中，以点C为旋转中心，将△ABC旋转到△A′B′C的位置，其中A′，B′分别是A，B的对应点，且点B′在AB边上，按照上述方法旋转△A′B′C，…，这样共旋转四次恰好构成一个旋转对称图形．（1）求∠BCB′的度数．
（2）判断△BCB′的形状．
分析 （1）根据旋转的性质可知旋转对称图形是正五边形，再根据正五边形的旋转角列式计算即可得解；
（2）根据旋转的性质可得CB=CB′，再根据等腰三角形的判定解答．
解答 解：（1）∵旋转四次恰好构成一个旋转对称图形，
∴旋转对称图形是正五边形，
∴∠BCB′=360°÷5=72°；
（2）∵△ABC旋转到△A′B′C的位置，
∴CB=CB′，
∴△BCB′是等腰三角形．
点评 本题考查旋转对称图形的概念：把一个图形绕着一个定点旋转一个角度后，与初始图形重合，这种图形叫做旋转对称图形，这个定点叫做旋转对称中心，旋转的角度叫做旋转角．
练习册系列答案
相关题目
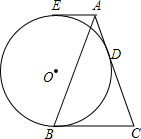如图，在△ABC中，AB=AC，半径为4的⊙O分别与直线BC，AC相切于点B，D，过点A作⊙O的切线，E为切点，当AE∥BC时，AE的长是2$\sqrt{2}$．
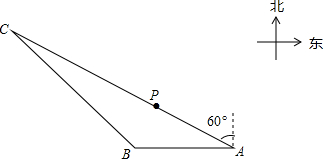如图．有一艘渔船P在捕鱼作业时出现故障，急需抢修，调度中心通知附近两个小岛A，B上的观测点进行观测，从观测站A测得渔船P在北偏西60°的方向，同时测得搜救船C也在北偏西60°的方向，从观测站B测得渔船P在北偏东32°的方向，测得搜救船C在北偏西45°方向，已知观测站A在观测站B东40里处，问搜救船C与渔船P的距离是多少？（结果保留整数，参考数据：sin32°≈0.53，cos32°≈0.85；tan32°≈0.62，sin58°≈0.85；cos58°≈0.53；tan58°≈1.60；$\sqrt{2}$≈1.41，$\sqrt{3}$≈1.73）．
在平面直角坐标系xOy中，直线y=$\frac{3}{4}$x+1与x轴交于点A，且与反比例函数y=$\frac{k}{x}$（x＞0）的图象交于点B（$\frac{8}{3}$，m）．
如图，点A，O，C在同一直线上，
如图，AB∥CD，NB、ND分别平分∠ABM和∠MDC，求证：∠M=2∠N．