题目内容
7.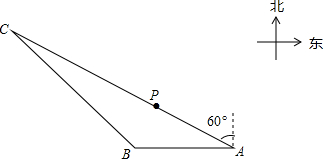 如图.有一艘渔船P在捕鱼作业时出现故障,急需抢修,调度中心通知附近两个小岛A,B上的观测点进行观测,从观测站A测得渔船P在北偏西60°的方向,同时测得搜救船C也在北偏西60°的方向,从观测站B测得渔船P在北偏东32°的方向,测得搜救船C在北偏西45°方向,已知观测站A在观测站B东40里处,问搜救船C与渔船P的距离是多少?(结果保留整数,参考数据:sin32°≈0.53,cos32°≈0.85;tan32°≈0.62,sin58°≈0.85;cos58°≈0.53;tan58°≈1.60;$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73).
如图.有一艘渔船P在捕鱼作业时出现故障,急需抢修,调度中心通知附近两个小岛A,B上的观测点进行观测,从观测站A测得渔船P在北偏西60°的方向,同时测得搜救船C也在北偏西60°的方向,从观测站B测得渔船P在北偏东32°的方向,测得搜救船C在北偏西45°方向,已知观测站A在观测站B东40里处,问搜救船C与渔船P的距离是多少?(结果保留整数,参考数据:sin32°≈0.53,cos32°≈0.85;tan32°≈0.62,sin58°≈0.85;cos58°≈0.53;tan58°≈1.60;$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73).
分析 过C作CD⊥AB于D,PE⊥AB于E,连接PB,根据已知条件得到BD=CD,AD=$\sqrt{3}$CD,求得CD=20($\sqrt{3}$+1)里,AD=40+20($\sqrt{3}$+1)里,解直角三角形得到PE≈12,即可得到结论.
解答  解:过C作CD⊥AB于D,PE⊥AB于E,连接PB,
解:过C作CD⊥AB于D,PE⊥AB于E,连接PB,
∴∠CBD=45°,∠CAD=30°,∠PBE=58°,
∴BD=CD,AD=$\sqrt{3}$CD,
∵AB=40里,
∴$\frac{CD}{40+CD}$=$\frac{\sqrt{3}}{3}$,
∴CD=20($\sqrt{3}$+1),
∴AD=40+20($\sqrt{3}$+1)里,
在Rt△PBE中,BE=$\frac{PE}{tan58°}$=$\frac{PE}{1.6}$,
在Rt△APE中,AE=$\sqrt{3}$PE,
∴$\frac{PE}{1.6}$+$\sqrt{3}$PE=40,
∴PE≈17,
∴AP=2PE=34,AC=2CD=40($\sqrt{3}$+1),
∴CP=AC-PC=109-34=75(里).
答:搜救船C与渔船P的距离是75里.
点评 本题考查的是解直角三角形的应用-方向角问题,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图1,AB是⊙O的直径,BC是⊙O的切线,OC∥弦AD,连接BD交AC于E.
如图1,AB是⊙O的直径,BC是⊙O的切线,OC∥弦AD,连接BD交AC于E.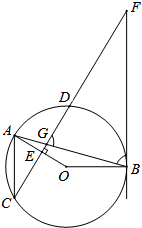 如图,在⊙O中,弦AB与弦CD相交于点G,OA⊥CD于点E,过点B的直线与CD的延长线交于点F,AC∥BF.
如图,在⊙O中,弦AB与弦CD相交于点G,OA⊥CD于点E,过点B的直线与CD的延长线交于点F,AC∥BF.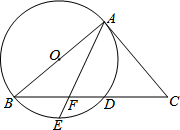 如图,以△ABC的边AB为直径作⊙O,与BC交于点D,点E是弧BD的中点,连接AE交BC于点F,∠ACB=2∠BAE.
如图,以△ABC的边AB为直径作⊙O,与BC交于点D,点E是弧BD的中点,连接AE交BC于点F,∠ACB=2∠BAE.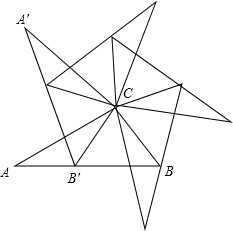 如图,在△ABC中,以点C为旋转中心,将△ABC旋转到△A′B′C的位置,其中A′,B′分别是A,B的对应点,且点B′在AB边上,按照上述方法旋转△A′B′C,…,这样共旋转四次恰好构成一个旋转对称图形.
如图,在△ABC中,以点C为旋转中心,将△ABC旋转到△A′B′C的位置,其中A′,B′分别是A,B的对应点,且点B′在AB边上,按照上述方法旋转△A′B′C,…,这样共旋转四次恰好构成一个旋转对称图形.