题目内容
10.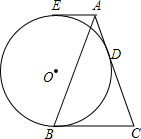 如图,在△ABC中,AB=AC,半径为4的⊙O分别与直线BC,AC相切于点B,D,过点A作⊙O的切线,E为切点,当AE∥BC时,AE的长是2$\sqrt{2}$.
如图,在△ABC中,AB=AC,半径为4的⊙O分别与直线BC,AC相切于点B,D,过点A作⊙O的切线,E为切点,当AE∥BC时,AE的长是2$\sqrt{2}$.
分析 如图连接BE、作AM⊥BC于M,先证明AB=AC=3AE,在RT△ABE中利用勾股定理即可解决问题.
解答 解:如图连接BE、作AM⊥BC于M,
∵AB=AC,AM⊥BC,
∴BM=MC,
∵AE、CB是切线,
∴∠AEB=∠EBC=90°,∵∠AMB=90°,
∴四边形AMBE是矩形,
∴AE=BM=MC,
∵AC是切线.
∴AE=AD,CB=CDM
∴AC=AE+BC=AE+2AE=3AE,设AE=a,则AB=AC=3a,
在RT△ABE中,∵AB2=BE2+AE2,
∴9a2=a2+82,
∴a=2$\sqrt{2}$,
∴AE=2$\sqrt{2}$.
故答案为2$\sqrt{2}$.
点评 本题考查切线的性质、切线长定理、勾股定理等知识,解题的关键是添加辅助线,学会常用辅助线的添加方法,属于中考常考题型.

练习册系列答案
相关题目

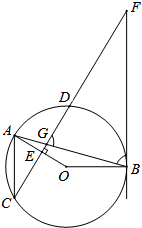 如图,在⊙O中,弦AB与弦CD相交于点G,OA⊥CD于点E,过点B的直线与CD的延长线交于点F,AC∥BF.
如图,在⊙O中,弦AB与弦CD相交于点G,OA⊥CD于点E,过点B的直线与CD的延长线交于点F,AC∥BF. 甲、乙两班离A地的距离分别为y1km,y2km,y1,y2与x(h)之间的函数关系如图所示,根据图象解答下列问题:
甲、乙两班离A地的距离分别为y1km,y2km,y1,y2与x(h)之间的函数关系如图所示,根据图象解答下列问题: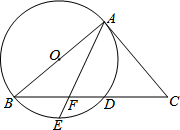 如图,以△ABC的边AB为直径作⊙O,与BC交于点D,点E是弧BD的中点,连接AE交BC于点F,∠ACB=2∠BAE.
如图,以△ABC的边AB为直径作⊙O,与BC交于点D,点E是弧BD的中点,连接AE交BC于点F,∠ACB=2∠BAE.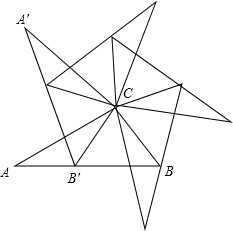 如图,在△ABC中,以点C为旋转中心,将△ABC旋转到△A′B′C的位置,其中A′,B′分别是A,B的对应点,且点B′在AB边上,按照上述方法旋转△A′B′C,…,这样共旋转四次恰好构成一个旋转对称图形.
如图,在△ABC中,以点C为旋转中心,将△ABC旋转到△A′B′C的位置,其中A′,B′分别是A,B的对应点,且点B′在AB边上,按照上述方法旋转△A′B′C,…,这样共旋转四次恰好构成一个旋转对称图形.