题目内容
8.一次函数经过点(2,3)和(0,4).(1)求一次函数的解析式;
(2)在平面直角坐标系中画出它的图象;
(3)当-2≤y≤2时,利用图象求x的取值范围.
分析 (1)设一次函数的解析式是y=kx+b,把(2,3)和(0,4)代入得出方程组,求出方程组的解即可;
(2)过点(2,3)和(0,4)作直线即可;
(3)根据图象得出答案即可.
解答 解:(1)设一次函数的解析式是y=kx+b,
把(2,3)和(0,4)代入得:$\left\{\begin{array}{l}{2k+b=3}\\{b=4}\end{array}\right.$,
解得:k=-$\frac{1}{2}$,b=4.
所以一次函数的解析式是y=-$\frac{1}{2}$x+4;
(2)过点(2,3)和(0,4)画直线,如图: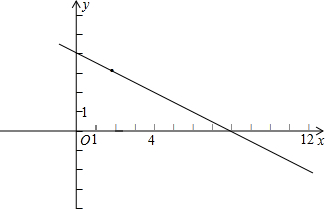
(3)当-2≤y≤2时,x的取值范围是4≤x≤12.
点评 本题考查了用待定系数法求一次函数的解析式,一次函数的性质和图象的应用,能求出函数的解析式是解此题的关键,数形结合思想的应用.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
11.学校准备用一笔钱买奖品,若以1支钢笔和2本日记本为一份奖品,则可购买80份奖品,若以一支钢笔和4本日记本为一份奖品,则可购买60份奖品,问若以1支钢笔和1本日记本为一份奖品,则可购买96份奖品.
19.在四边形ABCD中,AC与BD相交于点O,且OA=OC,OB=OD.如果再增加条件AC=BD,此四边形一定是( )
| A. | 正方形 | B. | 矩形 | C. | 菱形 | D. | 都有可能 |
16.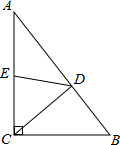 如图,在Rt△ABC中,∠ACB=90°,AB=5,BC=3,过点C作CD⊥AB,取AC的中点E,连接DE,则△DEC的周长是( )
如图,在Rt△ABC中,∠ACB=90°,AB=5,BC=3,过点C作CD⊥AB,取AC的中点E,连接DE,则△DEC的周长是( )
 如图,在Rt△ABC中,∠ACB=90°,AB=5,BC=3,过点C作CD⊥AB,取AC的中点E,连接DE,则△DEC的周长是( )
如图,在Rt△ABC中,∠ACB=90°,AB=5,BC=3,过点C作CD⊥AB,取AC的中点E,连接DE,则△DEC的周长是( )| A. | 2.4 | B. | 4.4 | C. | 6.4 | D. | 7 |
17.对于有理数a、b,定义a×b=3a+2b,则(x+y)×(x-y)×3x化简后得( )
| A. | 0 | B. | 5x | C. | 21x+3y | D. | 9x+5y |