题目内容
16．
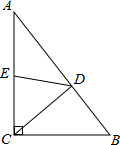如图，在Rt△ABC中，∠ACB=90°，AB=5，BC=3，过点C作CD⊥AB，取AC的中点E，连接DE，则△DEC的周长是（ ）| A． | 2.4 | B． | 4.4 | C． | 6.4 | D． | 7 |
分析 根据勾股定理求出AC的长，根据三角形的面积公式求出CD的长，根据直角三角形斜边上的中线等于斜边的一半求出DE，根据三角形的周长公式求出答案．
解答 解：∵∠ACB=90°，AB=5，BC=3，
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=4，
∵E为AC的中点，∴DE=$\frac{1}{2}$AC=2，又EC=$\frac{1}{2}$AC=2，
$\frac{1}{2}$×3×4=$\frac{1}{2}$×5×CD，CD=2.4，
∴△DEC的周长是EC+CD+CE=6.4，
故选：C．
点评 本题考查的是直角三角形的性质，掌握直角三角形斜边上的中线等于斜边的一半是解题的关键．
练习册系列答案
第三学期赢在暑假系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
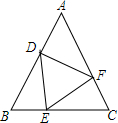已知，如图，△ABC中，AB=AC，动点D、E、F在AB、BC、AC上移动，移动过程中始终保持BD=CE，∠DEF=∠B，请你分析是否存在始终与△BDE全等的三角形，并说明理由．
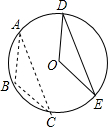如图，△ABC是⊙O的内接三角形，平移△ABC使点B与圆心O重合，A、C两点恰好落在圆上的D、E两点处．若AC=2$\sqrt{3}$，则平移的距离为2．