题目内容
1.已知:△ABC是等腰直角三角形,四边形BDEF是正方形,P是EC的中点.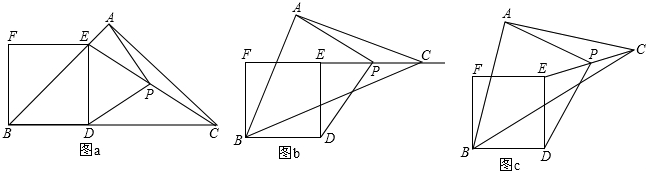
(1)如图a,当B、D、C在同一直线上时,请探究PA和PD的数量关系有PA=PD,位置关系有PA⊥PD.
(2)如图b,把等腰直角△ABC绕点B逆时针旋转,当点C恰好在射线FE上时:
问题①:(1)中得到的结论还成立吗?请加以证明.
问题②:若正方形BDEF的面积为1,等腰直角△ABC的面积为y,PC的长为x,求y关于x的函数关系式.
(3)如图c,把等腰直角△ABC绕点B逆时针旋转到一般位置时,请直接写出(1)中得到的结论一定成立(填“成立”或“不成立”).
分析 (1)根据直角三角形斜边的中线的性质求得PA=PC,∠PAC=∠PCA,PD=PC,∠PCD=∠PDC,进而就可证得PA=PD,PA⊥PD.
(2),在BF上截取BG=CP,连接AG、DG,先证得△ABG≌△ACP,得出AG=AP,∠BAG=∠CAP,进而证得∠GAP=90°,再证得△DBG≌△DEP,得出DG=DP,∠BDG=∠EDP进而证得∠GDP=90°,然后证得四边形AGDP是正方形,即可证得PA=PD,PA⊥PD.
(3)将△PDE绕D点逆时针旋转90°,使E和B重合,P到G位置,连接AG,然后证得△AGB≌△APC,得出AG=AP,∠GAB=∠PAC,进而证得∠GAP=90°,然后证得四边形AGDP是正方形,即可证得PA=PD,PA⊥PD.
解答 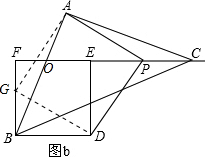 解:(1)∵△ABC是等腰直角三角形,
解:(1)∵△ABC是等腰直角三角形,
∴∠EAC=90°,
∵P是EC的中点,
∴PA=PC,
∴∠PAC=∠PCA,
∵四边形BDEF是正方形,
∴∠EDC=90°,
同理证得:PD=PC,∠PCD=∠PDC,
∵∠ACP+∠PCD=∠ACB=45°,
∴∠APD=∠PAC+∠PCA+∠PCD+∠PDC=2∠ACB=90°,
∴PA⊥PD,
故答案为:PA=PD,PA⊥PD.
(2)①成立;
如图b,在BF上截取BG=CP,连接AG、DG,
∵∠BAC=∠F=90°,∠AOC=∠BOF,
∴∠FBA=∠ACP,
在△ABG和△ACP中,
$\left\{\begin{array}{l}{AB=AC}\\{∠ABG=∠ACP}\\{BG=CP}\end{array}\right.$,
∴△ABG≌△ACP(SAS),
∴AG=AP,∠BAG=∠CAP,
∵∠BAC=90°,
∴∠GAP=90°,
∵BG=CP,EP=CP,
∴GB=EP,
在△DBG和△DEP中,
$\left\{\begin{array}{l}{BG=EP}\\{∠DBG=∠DEP=90°}\\{BD=DE}\end{array}\right.$,
∴△DBG≌△DEP(SAS),
∴DG=DP,∠BDG=∠EDP,
∵∠BDE=90°,
∴∠GDP=90°,
∴∠AGP=∠APG=∠DGP=∠DPG=45°,
∴∠AGD=∠APD=90°,
∴四边形AGDP是正方形,
∴PA=PD,PA⊥PD,
(3)成立;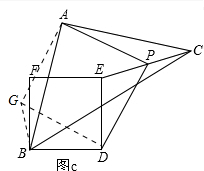 如图c,将△PDE绕D点逆时针旋转90°,使E和B重合,P到G位置,连接AG,
如图c,将△PDE绕D点逆时针旋转90°,使E和B重合,P到G位置,连接AG,
则∠DGB=∠DPE,∠PDE=∠GDB,DG=DP,
∵∠APE=90°-∠EPD,
∴∠APC=180°-∠APE=90°+∠EPD,
∵∠AGB=90°+∠DGB,
∴∠AGB=∠APC,
在△AGB和△APC中,
$\left\{\begin{array}{l}{GB=PC}\\{∠AGB=∠APC}\\{AB=AC}\end{array}\right.$,
∴△AGB≌△APC(SAS),
∴AG=AP,∠GAB=∠PAC,
∴∠GAP=90°,
∴四边形AGDP是正方形,
∴PA=PD,PA⊥PD.
点评 本题考查了等腰直角三角形的性质,直角三角形斜边中线的性质,正方形的判定和性质,三角形全等的判定和性质,找出全等三角形是解题的关键.

 名校课堂系列答案
名校课堂系列答案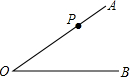 如图,P为∠AOB边OA上一点,∠AOB=30°,OP=10cm,以P为圆心,5cm为半径的圆与直线OB的位置关系是( )
如图,P为∠AOB边OA上一点,∠AOB=30°,OP=10cm,以P为圆心,5cm为半径的圆与直线OB的位置关系是( )| A. | 相离 | B. | 相交 | C. | 相切 | D. | 无法确定 |
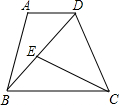 如图,在梯形ABCD中,AD∥BC,点E在对角线BD上,且∠DCE=∠ADB,如果BC=9,CD:BD=2:3,求CE的长.
如图,在梯形ABCD中,AD∥BC,点E在对角线BD上,且∠DCE=∠ADB,如果BC=9,CD:BD=2:3,求CE的长.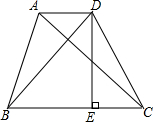 如图,在等腰梯形ABCD中,AD∥BC,AB=CD,且AC⊥BD,DE是梯形的高,若S梯形ABCD=49cm2,求梯形的高.
如图,在等腰梯形ABCD中,AD∥BC,AB=CD,且AC⊥BD,DE是梯形的高,若S梯形ABCD=49cm2,求梯形的高.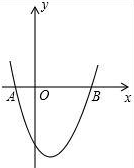 如图,抛物线y=x2-x-2交x轴于A(-1,0),B两点,交y轴于C(0,-2),过A,C画直线.点M在抛物线上,以M为圆心的圆与直线AC相切,切点为H,若⊙M的半径为$\frac{4\sqrt{5}}{5}$,求点M的坐标.
如图,抛物线y=x2-x-2交x轴于A(-1,0),B两点,交y轴于C(0,-2),过A,C画直线.点M在抛物线上,以M为圆心的圆与直线AC相切,切点为H,若⊙M的半径为$\frac{4\sqrt{5}}{5}$,求点M的坐标.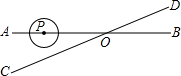 如图,直线AB、CD相交于点O,∠AOC=30°,半径为1cm的⊙P的圆心在射线OA上,且与点O的距离为6cm,如果⊙P以1cm/s的速度沿由A向B的方向移动,那么⊙P与直线CD相切时运动时间为( )
如图,直线AB、CD相交于点O,∠AOC=30°,半径为1cm的⊙P的圆心在射线OA上,且与点O的距离为6cm,如果⊙P以1cm/s的速度沿由A向B的方向移动,那么⊙P与直线CD相切时运动时间为( ) 如图,正方形ABCD的正方形CEFG的面积分别是7和5.
如图,正方形ABCD的正方形CEFG的面积分别是7和5.