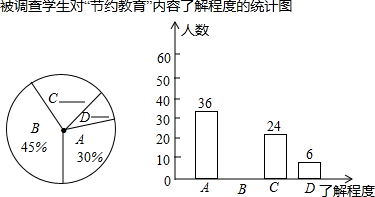
题目内容
1．
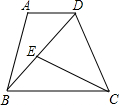如图，在梯形ABCD中，AD∥BC，点E在对角线BD上，且∠DCE=∠ADB，如果BC=9，CD：BD=2：3，求CE的长．
分析 先证明∠DCE=∠BDC，再由公共角，证明△CDE∽△BDC，得出对应边成比例，即可求出CE．
解答 解：∵AD∥BC，
∴∠ADB=∠CBD，
∵∠DCE=∠ADB，
∴∠DCE=∠CBD，
又∵∠CDE=∠BDC，
∴△CDE∽△BDC，
∴$\frac{CE}{BC}=\frac{CD}{BD}$=$\frac{2}{3}$，
即$\frac{CE}{9}=\frac{2}{3}$，
∴CE=6．
点评 本题考查了梯形的性质、相似三角形的判定与性质；证明三角形相似是解决问题的关键．
练习册系列答案
快捷英语周周练系列答案
相关题目
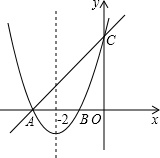已知：如图，抛物线y1=a（x-h） 2+k与直线y2=k′x+b分别交于x轴和y轴上的点A（-3，0）和点C（0，3），已知抛物线的对称轴为直线x=-2．
9．|-$\frac{2}{3}$|=（ ）
| A． | -$\frac{2}{3}$ | B． | $\frac{2}{3}$ | C． | $\frac{3}{2}$ | D． | -$\frac{3}{2}$ |
