题目内容
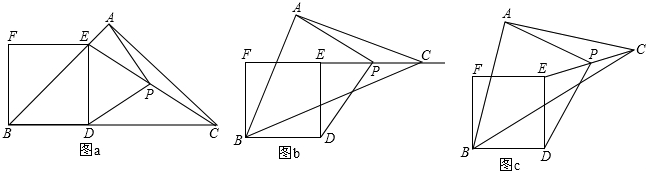
11. 如图,正方形ABCD的正方形CEFG的面积分别是7和5.
如图,正方形ABCD的正方形CEFG的面积分别是7和5.求:(1)S△BEF;(2)S△BDF.
分析 (1)求得正方形ABCD的正方形CEFG边长,△BEF是底为两个正方形的边长和,高为小正方形的边长,由此列式求的面积即可;
(2)连接CF,△BCF和△DCF等底等高(底和高分别等于大、小正方形的边长),则二者的面积相等,分别去掉公共部分(△CFH),那么剩余的部分的面积,仍然相等,即△BCH和△HFD的面积相等,于是阴影部分的面积就变成了大正方形的面积的一半,据此代入数据即可求解.
解答 解:(1)∵正方形ABCD的正方形CEFG的面积分别是7和5.
∴正方形ABCD的正方形CEFG边长分别为$\sqrt{7}$,$\sqrt{5}$,
∴S△BEF=$\frac{1}{2}$(BC+CE)•EF=$\frac{1}{2}$($\sqrt{7}$+$\sqrt{5}$)×$\sqrt{5}$=$\frac{5}{2}$+$\frac{\sqrt{35}}{2}$;
(2)如图,
连接CF,
∵S△BCF=S△DCF,
∴S△BCF-S△CFH=S△DCF-S△CFH,
即S△BCH=S△HFD,
∴S△BDF=$\frac{1}{2}$S正方形ABCD=$\frac{7}{2}$.
点评 此题考查正方形的性质,每一条边都相等,三角形的面积计算方法,结合图形,适当转化问题是解决问题的关键.

练习册系列答案
相关题目
19.若x轴上的点P到y轴的距离为2015,则点P的坐标是( )
| A. | (2015,0) | B. | (0,2015) | C. | (2015,0)或(-2015,0) | D. | (0,2015)或(0,-2015) |
6.下面调查中,适合采用普查的事件是( )
| A. | 对全国中学生心理健康现状的调查 | |
| B. | 对我市食品合格情况的调查 | |
| C. | 对江苏卫视《最强大脑》收视率的调查 | |
| D. | 对你所在班级同学身高情况的调查 |
3.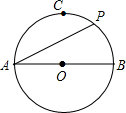 如图,在⊙O中,AB是直径,点C是$\widehat{AB}$的中点,点P是$\widehat{BC}$上任意一点,则∠PAB的度数不可能为( )
如图,在⊙O中,AB是直径,点C是$\widehat{AB}$的中点,点P是$\widehat{BC}$上任意一点,则∠PAB的度数不可能为( )
 如图,在⊙O中,AB是直径,点C是$\widehat{AB}$的中点,点P是$\widehat{BC}$上任意一点,则∠PAB的度数不可能为( )
如图,在⊙O中,AB是直径,点C是$\widehat{AB}$的中点,点P是$\widehat{BC}$上任意一点,则∠PAB的度数不可能为( )| A. | 0° | B. | 30° | C. | 45° | D. | 60° |