题目内容
5．
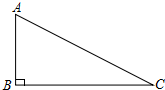如图，△ABC中，∠B=90°，AB=1，BC=2，则cosA=（ ）| A． | $\frac{{\sqrt{5}}}{5}$ | B． | $\frac{{\sqrt{3}}}{3}$ | C． | $\frac{{2\sqrt{5}}}{5}$ | D． | $\frac{1}{2}$ |
分析 根据勾股定理，可得AC的长，根据余弦等于邻边比斜边，可得答案．
解答 解：由勾股定理，得
AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{5}$．
cosA=$\frac{AB}{AC}$=$\frac{1}{\sqrt{5}}$=$\frac{\sqrt{5}}{5}$，
故选：A．
点评 本题考查了锐角三角函数，利用勾股定理AC的长是解题关键．
练习册系列答案
相关题目
16．将分式方程$\frac{x}{x-3}=2-\frac{3}{3-x}$去分母得（ ）
| A． | x=2+3 | B． | x=2（x-3）+3 | C． | x=2（x-3）+3（x-3） | D． | x=2（x-3）-3 |
如图，直线l1∥l2，∠2=40°，则∠1+∠3+∠4=220°．
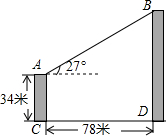如图，甲、乙两栋大楼相距78米，一测量人员从甲楼AC的顶部看乙楼BD的顶部其仰角为27°．如果甲楼的高为34米，求乙楼的高度是多少米？（结果精确到0.1米）
14．如果一个多边形的外角分别是10°，20°，30°…，那么这个多边形是（ ）
| A． | 六边形 | B． | 七边形 | C． | 八边形 | D． | 九边形 |
如图是一个物体的三视图，根据图中尺寸（单位：cm），它的体积为32+8πcm3．