题目内容
6.函数y=$\frac{1}{x-2}$的自变量x的取值范围为( )| A. | x>2 | B. | x<2 | C. | x≤2 | D. | x≠2 |
分析 根据当函数表达式的分母中含有自变量时,自变量取值要使分母不为零,判断求解即可.
解答 解:∵函数表达式y=$\frac{1}{x-2}$的分母中含有自变量x,
∴自变量x的取值范围为:x-2≠0,
即x≠2.
故选D.
点评 本题考查了函数自变量取值范围的知识,求自变量的取值范围的关键在于必须使含有自变量的表达式都有意义.

练习册系列答案
相关题目
16.某文具店三月份销售铅笔100支,四、五两个月销售量连续增长.若月平均增长率为x,则该文具店五月份销售铅笔的支数是( )
| A. | 100(1+x) | B. | 100(1+x)2 | C. | 100(1+x2) | D. | 100(1+2x) |
14.已知x2-3x-4=0,则代数式$\frac{x}{{{x^2}-x-4}}$的值是( )
| A. | 3 | B. | 2 | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
11.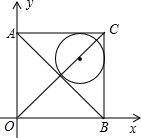 如图,在平面直角坐标系中有一正方形AOBC,反比例函数y=$\frac{k}{x}$经过正方形AOBC对角线的交点,半径为4-2$\sqrt{2}$的圆内切于△ABC,则k的值为( )
如图,在平面直角坐标系中有一正方形AOBC,反比例函数y=$\frac{k}{x}$经过正方形AOBC对角线的交点,半径为4-2$\sqrt{2}$的圆内切于△ABC,则k的值为( )
 如图,在平面直角坐标系中有一正方形AOBC,反比例函数y=$\frac{k}{x}$经过正方形AOBC对角线的交点,半径为4-2$\sqrt{2}$的圆内切于△ABC,则k的值为( )
如图,在平面直角坐标系中有一正方形AOBC,反比例函数y=$\frac{k}{x}$经过正方形AOBC对角线的交点,半径为4-2$\sqrt{2}$的圆内切于△ABC,则k的值为( )| A. | $\sqrt{2}$ | B. | 2 | C. | 4 | D. | 2$\sqrt{2}$ |
 如图,⊙O的直径AB过弦CD的中点E,若∠C=25°,则∠D=65°.
如图,⊙O的直径AB过弦CD的中点E,若∠C=25°,则∠D=65°.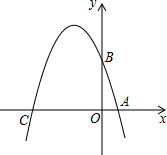 已知如图,在平面直角坐标系xOy中,点A、B、C分别为坐标轴上的三个点,且OA=1,OB=3,OC=4,
已知如图,在平面直角坐标系xOy中,点A、B、C分别为坐标轴上的三个点,且OA=1,OB=3,OC=4, 如图是由4个完全相同的小正方体组成的立体图形,则它的俯视图是( )
如图是由4个完全相同的小正方体组成的立体图形,则它的俯视图是( )



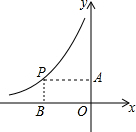 如图,点P是反比例函数$y=\frac{k}{x}$(x<0)图象的一点,PA垂直于y轴,垂足为点A,PB垂直于x轴,垂足为点B.若矩形PBOA的面积为6,则k的值为-6.
如图,点P是反比例函数$y=\frac{k}{x}$(x<0)图象的一点,PA垂直于y轴,垂足为点A,PB垂直于x轴,垂足为点B.若矩形PBOA的面积为6,则k的值为-6.