题目内容
2.某单位购买甲、乙两种纯净水共用240元,其中甲种水每桶8元,乙种水每桶6元;乙种水的桶数是甲种水桶数的$\frac{1}{3}$.则购买甲、乙两种水一共32桶.分析 根据关键描述语是:甲、乙两种纯净水共用240元;乙种水的桶数是甲种水桶数的$\frac{1}{3}$.可得等量关系为:①甲种水的桶数是×8+乙种水桶数×6=240;②乙种水的桶数=甲种水桶数×$\frac{1}{3}$.则设买甲种水x桶,买乙种水y桶,根据等量关系可列方程组.
解答 解:设买甲种水x桶,买乙种水y桶,
列方程$\left\{\begin{array}{l}{8x+6y=240}\\{y=\frac{1}{3}x}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=24}\\{y=8}\end{array}\right.$,
即x+y=24+8=32,
故答案为32.
点评 本题主要考查了二元一次方程组的应用,根据实际问题中的条件列方程组时,要注意抓住题目中的一些关键性词语,找出等量关系,列出方程组.

练习册系列答案
相关题目
8.以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
5.要使二次根式$\sqrt{x-3}$有意义,则x的取值范围是( )
| A. | x≠3 | B. | x>3 | C. | x≤3 | D. | x≥3 |
12.下列性质中菱形不一定具有的性质是( )
| A. | 对角线互相平分 | B. | 对角线互相垂直 | ||
| C. | 对角线相等 | D. | 既是轴对称图形又是中心对称图形 |
11.定义一种新运算:a?b=a(a-b),例如,4?3=4×(4-3)=4,若x?2=3,则x的值是( )
| A. | x=3 | B. | x=-1 | C. | x1=3,x2=1 | D. | x1=3,x2=-1 |
12.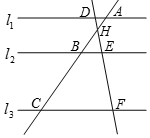 如图,直线l1∥l2∥l3,直线AC分别交l1、l2、l3于点A、B、C,直线DF分别交l1、l2、l3于点D、E、F,AC与DF相交于点H,则下列式子不正确的是( )
如图,直线l1∥l2∥l3,直线AC分别交l1、l2、l3于点A、B、C,直线DF分别交l1、l2、l3于点D、E、F,AC与DF相交于点H,则下列式子不正确的是( )
 如图,直线l1∥l2∥l3,直线AC分别交l1、l2、l3于点A、B、C,直线DF分别交l1、l2、l3于点D、E、F,AC与DF相交于点H,则下列式子不正确的是( )
如图,直线l1∥l2∥l3,直线AC分别交l1、l2、l3于点A、B、C,直线DF分别交l1、l2、l3于点D、E、F,AC与DF相交于点H,则下列式子不正确的是( )| A. | $\frac{AB}{BC}$=$\frac{DE}{EF}$ | B. | $\frac{AB}{DE}$=$\frac{BC}{EF}$ | C. | $\frac{AB}{AC}$=$\frac{DE}{DF}$ | D. | $\frac{AB}{BC}$=$\frac{BE}{CF}$ |