题目内容
8.以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是( )| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
分析 由于内接正三角形、正方形、正六边形是特殊内角的多边形,可构造直角三角形分别求出边心距的长,由勾股定理逆定理可得该三角形是直角三角形,进而可得其面积.
解答 解:如图1,
∵OC=2,
∴OD=2×sin30°=1;
如图2,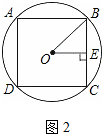
∵OB=2,
∴OE=2×sin45°=$\sqrt{2}$;
如图3,
∵OA=2,
∴OD=2×cos30°=$\sqrt{3}$,
则该三角形的三边分别为:1,$\sqrt{2}$,$\sqrt{3}$,
∵(1)2+($\sqrt{2}$)2=($\sqrt{3}$)2,
∴该三角形是直角三角形,
∴该三角形的面积是:$\frac{1}{2}$×1×$\sqrt{2}$=$\frac{\sqrt{2}}{2}$.
故选:A.
点评 本题主要考查多边形与圆,解答此题要明确:多边形的半径、边心距、中心角等概念,根据解直角三角形的知识解答是解题的关键.

练习册系列答案
相关题目
19.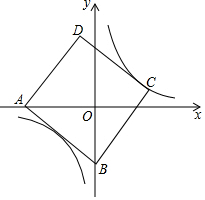 如图,正方形ABCD的边长为5,点A的坐标为(-4,0),点B在y轴上,若反比例函数y=$\frac{k}{x}$(k≠0)的图象过点C,则该反比例函数的表达式为( )
如图,正方形ABCD的边长为5,点A的坐标为(-4,0),点B在y轴上,若反比例函数y=$\frac{k}{x}$(k≠0)的图象过点C,则该反比例函数的表达式为( )
 如图,正方形ABCD的边长为5,点A的坐标为(-4,0),点B在y轴上,若反比例函数y=$\frac{k}{x}$(k≠0)的图象过点C,则该反比例函数的表达式为( )
如图,正方形ABCD的边长为5,点A的坐标为(-4,0),点B在y轴上,若反比例函数y=$\frac{k}{x}$(k≠0)的图象过点C,则该反比例函数的表达式为( )| A. | y=$\frac{3}{x}$ | B. | y=$\frac{4}{x}$ | C. | y=$\frac{5}{x}$ | D. | y=$\frac{6}{x}$ |
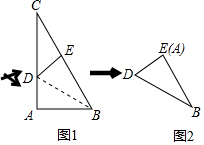 在三角形纸片ABC中,∠A=90°,∠C=30°,AC=30cm,将该纸片沿过点B的直线折叠,使点A落在斜边BC上的一点E处,折痕记为BD(如图1),减去△CDE后得到双层△BDE(如图2),再沿着过△BDE某顶点的直线将双层三角形剪开,使得展开后的平面图形中有一个是平行四边形,则所得平行四边形的周长为40或$\frac{80\sqrt{3}}{3}$cm.
在三角形纸片ABC中,∠A=90°,∠C=30°,AC=30cm,将该纸片沿过点B的直线折叠,使点A落在斜边BC上的一点E处,折痕记为BD(如图1),减去△CDE后得到双层△BDE(如图2),再沿着过△BDE某顶点的直线将双层三角形剪开,使得展开后的平面图形中有一个是平行四边形,则所得平行四边形的周长为40或$\frac{80\sqrt{3}}{3}$cm.