题目内容
12.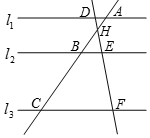 如图,直线l1∥l2∥l3,直线AC分别交l1、l2、l3于点A、B、C,直线DF分别交l1、l2、l3于点D、E、F,AC与DF相交于点H,则下列式子不正确的是( )
如图,直线l1∥l2∥l3,直线AC分别交l1、l2、l3于点A、B、C,直线DF分别交l1、l2、l3于点D、E、F,AC与DF相交于点H,则下列式子不正确的是( )| A. | $\frac{AB}{BC}$=$\frac{DE}{EF}$ | B. | $\frac{AB}{DE}$=$\frac{BC}{EF}$ | C. | $\frac{AB}{AC}$=$\frac{DE}{DF}$ | D. | $\frac{AB}{BC}$=$\frac{BE}{CF}$ |
分析 根据平行线分线段成比例定理得到$\frac{AB}{BC}$=$\frac{DE}{EF}$或$\frac{AB}{AC}$=$\frac{DE}{DF}$,然后利用比例性质得到$\frac{AB}{DE}$=$\frac{BC}{EF}$,于是可对各选项进行判断.
解答 解:∵l1∥l2∥l3,
∴$\frac{AB}{BC}$=$\frac{DE}{EF}$或$\frac{AB}{AC}$=$\frac{DE}{DF}$
∴$\frac{AB}{DE}$=$\frac{BC}{EF}$.
故选D.
点评 本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
17.如图,是轴对称图形但不是中心对称图形的是( )
| A. |  线段 | B. |  等边三角形 | C. |  正方形 | D. |  圆 |
4.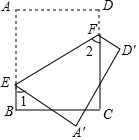 如图,E、F分别是矩形ABCD边AB、CD上的点,将矩形ABCD沿EF折叠,使A、D分别落在A′和D′处,若∠1=50°,则∠2的度数是( )
如图,E、F分别是矩形ABCD边AB、CD上的点,将矩形ABCD沿EF折叠,使A、D分别落在A′和D′处,若∠1=50°,则∠2的度数是( )
 如图,E、F分别是矩形ABCD边AB、CD上的点,将矩形ABCD沿EF折叠,使A、D分别落在A′和D′处,若∠1=50°,则∠2的度数是( )
如图,E、F分别是矩形ABCD边AB、CD上的点,将矩形ABCD沿EF折叠,使A、D分别落在A′和D′处,若∠1=50°,则∠2的度数是( )| A. | 65° | B. | 60° | C. | 50° | D. | 40° |
1.某快递公司的快件付费主要根据快件的质量按以下资费标准进行计算,即某地快件付费=该地首重+续重(快件质量-1kg)×该地续重资费.
(1)某同学寄物品给外地务工的父亲共付费用58元,且物品快件质量在10kg以上,20kg以下,请问该同学寄往何处?物品快件的质量是多少?请利用方程解决问题;
(2)如果他要寄特产给在北京的哥哥,且费用控制在40元以内,那么他最多可寄特产快件多少干克(结果取整数)?
| 快件到达地 | 首重现付资费(1kg) | 续重现付资费(每kg) |
| 江西 | 10 | 2 |
| 浙江、上海、广东等 | 12 | 4 |
| 北京、天津、山东等 | 15 | 6 |
(2)如果他要寄特产给在北京的哥哥,且费用控制在40元以内,那么他最多可寄特产快件多少干克(结果取整数)?
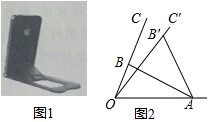 如图1是手机放在手机支架上,其侧面示意图如图2所示,AB,CD是长度不变的活动片,一端A固定在0A上,另一端B可在OC上变动位置,若将AB变到AB′的位置,则0C旋转一定角度到达OC′的位置.已知OA=8cm,AB⊥OC,∠BOA=60°,sin∠B′AO=$\frac{9}{10}$,则点B′到OA的距离$\frac{18\sqrt{3}}{5}$cm.
如图1是手机放在手机支架上,其侧面示意图如图2所示,AB,CD是长度不变的活动片,一端A固定在0A上,另一端B可在OC上变动位置,若将AB变到AB′的位置,则0C旋转一定角度到达OC′的位置.已知OA=8cm,AB⊥OC,∠BOA=60°,sin∠B′AO=$\frac{9}{10}$,则点B′到OA的距离$\frac{18\sqrt{3}}{5}$cm.