题目内容
1.已知关于x的一元二次方程x2+(k+1)x+$\frac{1}{2}$k-1=0(1)求证:不论k为何实数,方程总会有两个不相等的实数根;
(2)当k=4时,用配方法解出这个一元二次方程.
分析 (1)先进行判别式得到△=(k+1)2-4($\frac{1}{2}$k-1),再根据非负数的性质得到△>0,然后根据判别式的意义即可得到结论;
(2)代入k的值得出一元二次方程,用配方法解方程即可.
解答 (1)证明:△=(k+1)2-4($\frac{1}{2}$k-1)=k2+5,
∵k2≥0,
∴k2+5>0,
∴不论k为何实数,方程总会有两个不相等的实数根;
(2)解:当k=4时,方程为x2+5x+3=0,
x2+5x+$\frac{25}{4}$=$\frac{25}{4}$-3
(x+$\frac{5}{2}$)2=$\frac{13}{4}$
x+$\frac{5}{2}$=±$\frac{\sqrt{13}}{2}$
x1=-$\frac{5}{2}$+$\frac{\sqrt{13}}{2}$,x2=-$\frac{5}{2}$-$\frac{\sqrt{13}}{2}$.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.以及利用配方法解一元二次方程.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
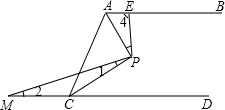 如图,AB∥CD,PA平分∠BAC,PC平分∠ACD,过P点作PM、PE交CD于M,交AB于E
如图,AB∥CD,PA平分∠BAC,PC平分∠ACD,过P点作PM、PE交CD于M,交AB于E