题目内容
16. 如图,已知OQ平分∠AOB,点P为OQ上任意一点,点N为OA上一点,点M为OB上一点,若∠PNO+∠PMO=180°,则PM和PN的大小关系是( )
如图,已知OQ平分∠AOB,点P为OQ上任意一点,点N为OA上一点,点M为OB上一点,若∠PNO+∠PMO=180°,则PM和PN的大小关系是( )| A. | PM>PN | B. | PM<PN | C. | PM=PN | D. | 不能确定 |
分析 作PE⊥OB于E,PF⊥OA于F,根据角平分线的性质定理证明PE=PF,根据三角形全等的判定定理证明△PFN≌△PEM,得到答案.
解答  解:作PE⊥OB于E,PF⊥OA于F,
解:作PE⊥OB于E,PF⊥OA于F,
∵OQ平分∠AOB,
∴PE=PF,
∵∠PNO+∠PNA=180°,∠PNO+∠PMO=180°,
∴∠PNA=∠PMO,
在△PFN和△PEM中,
$\left\{\begin{array}{l}{∠PNA=∠PMO}\\{∠PFN=∠PEM}\\{PF=PM}\end{array}\right.$$\left\{\begin{array}{l}{∠PFN=∠PEN}\\{∠PNA=∠PMO}\\{PN=PM}\end{array}\right.$,
∴△PFN≌△PEM,
∴PM=PN.
故选:C.
点评 本题考查的是角平分线的性质和全等三角形的判定和性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
相关题目
6.下列关于$\sqrt{2}$的说法中,错误的是( )
| A. | $\sqrt{2}$是无理数 | B. | 1<$\sqrt{2}$<2 | ||
| C. | $\sqrt{2}$是2的算术平方根 | D. | 2的平方根是$\sqrt{2}$ |
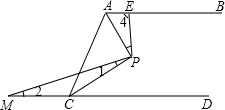 如图,AB∥CD,PA平分∠BAC,PC平分∠ACD,过P点作PM、PE交CD于M,交AB于E
如图,AB∥CD,PA平分∠BAC,PC平分∠ACD,过P点作PM、PE交CD于M,交AB于E 如图所示,在△ABC中,已知∠A=90°,BD平分∠ABC,AD=6cm,BC=15cm,求△BDC的面积.
如图所示,在△ABC中,已知∠A=90°,BD平分∠ABC,AD=6cm,BC=15cm,求△BDC的面积. 如图,画一个三角形,使它与△ABC相似,且相似比为1:2.
如图,画一个三角形,使它与△ABC相似,且相似比为1:2.