题目内容
等腰△ABC三边分别为a,b,c,且满足
=2,
=0,求△ABC的周长.
| 3 | a |
| c-b-2 |
考点:等腰三角形的性质,算术平方根,立方根,三角形三边关系
专题:
分析:先根据立方根、算术平方根的概念得到a=8,c=b+2,再分b是底边,b是腰两种情况,进行分类讨论.
解答:解:根据题意得a=8,c=b+2,
当a=c时,则8=b+2,解得b=6,
所以△ABC的周长=8+8+6=20;
当a=b时,则c=8+2=10,
所以△ABC的周长=8+8+10=26.
当a=c时,则8=b+2,解得b=6,
所以△ABC的周长=8+8+6=20;
当a=b时,则c=8+2=10,
所以△ABC的周长=8+8+10=26.
点评:本题考查了立方根、算术平方根、等腰三角形的性质和三角形的三边关系;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要,也是解题的关键.

练习册系列答案
相关题目
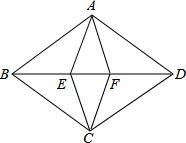 如图,四边形ABCD和四边形AECF都是菱形,点E、F在BD上,已知∠BAD=110°,∠EAF=50°,求:
如图,四边形ABCD和四边形AECF都是菱形,点E、F在BD上,已知∠BAD=110°,∠EAF=50°,求: 如图,已知正六边形ABCDEF的面积为a,AB、CD、EF所在的直线围成△PQR,求△PQR的面积.
如图,已知正六边形ABCDEF的面积为a,AB、CD、EF所在的直线围成△PQR,求△PQR的面积. 如图,圆心O与△ABC分别截于DE、FG、HM,且DE=FG=HM,若∠A=70°,求∠BOC的度数.
如图,圆心O与△ABC分别截于DE、FG、HM,且DE=FG=HM,若∠A=70°,求∠BOC的度数.