题目内容
 如图,圆心O与△ABC分别截于DE、FG、HM,且DE=FG=HM,若∠A=70°,求∠BOC的度数.
如图,圆心O与△ABC分别截于DE、FG、HM,且DE=FG=HM,若∠A=70°,求∠BOC的度数.考点:角平分线的性质,三角形内角和定理,垂径定理
专题:
分析:根据在同圆或等圆中等弦所对的弦心距相等可得点O到AB、BC、AC的距离相等,再根据到角的两边距离相等的点在角的平分线上可得BO、CO分别平分∠ABC和∠ACB,然后根据三角形的内角和定理求出∠ABC+∠ACB,再根据角平分线的定义求出∠OBC+∠OCB,再次利用三角形的内角和定理列式计算即可得解.
解答:解:∵DE=FG=HM,
∴点O到AB、BC、AC的距离相等,
∴BO、CO分别平分∠ABC和∠ACB,
∵∠A=70°,
∴∠ABC+∠ACB=180°-70°=110°,
∴∠OBC+∠OCB=
(∠ABC+∠ACB)=
×110°=55°,
在△BOC中,∠BOC=180°-(∠OBC+∠OCB)=180°-55°=125°.
∴点O到AB、BC、AC的距离相等,
∴BO、CO分别平分∠ABC和∠ACB,
∵∠A=70°,
∴∠ABC+∠ACB=180°-70°=110°,
∴∠OBC+∠OCB=
| 1 |
| 2 |
| 1 |
| 2 |
在△BOC中,∠BOC=180°-(∠OBC+∠OCB)=180°-55°=125°.
点评:本题考查了到角的两边距离相等的点在角的平分线上,三角形内角和定理,垂径定理,熟记在同圆或等圆中等弦所对的弦心距相等得到点O到AB、BC、AC的距离相等是解题的关键.

练习册系列答案
相关题目
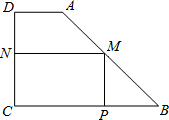 如图所示,有一块形状是直角梯形的铁皮ABCD,它的上底AD=15cm,下底BC=40cm,垂直于底的腰CD=30cm,现要截成一块矩形铁皮MPCN,使它的顶点M、P、N分别在AB、BC、CD边上,求矩形MPCN的面积S关于MN的长x的函数关系式.
如图所示,有一块形状是直角梯形的铁皮ABCD,它的上底AD=15cm,下底BC=40cm,垂直于底的腰CD=30cm,现要截成一块矩形铁皮MPCN,使它的顶点M、P、N分别在AB、BC、CD边上,求矩形MPCN的面积S关于MN的长x的函数关系式.