题目内容
 如图,抛物线y=ax2-5ax+b+
如图,抛物线y=ax2-5ax+b+| 2 |
| 5 |
| 1 |
| 2 |
考点:二次函数的性质
专题:
分析:首先求得两个函数的解析式,然后假设点D的横坐标为t(-3<t<5),因为点D在抛物线y=ax2-5ax+b+
上,所以点D的纵坐标为-
t2+
t+4.再过点D作y轴的平行线交AB于E.因而点D、点E的横坐标相同,且纵坐标可以通过直线AB的解析式表示出来.因而S△DAB就可以通过DE的距离(点D、E纵坐标的差值的绝对值)与点A、B横坐标的差值绝对值表示出来.
| 5 |
| 2 |
| 1 |
| 6 |
| 5 |
| 6 |
解答: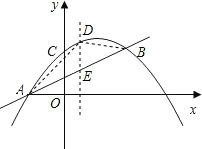 解:将A(-3,0)代入y=
解:将A(-3,0)代入y=
x+b,y=ax2-5ax+b+
,
得b=
,a=-
,
则抛物线解析式为y=-
x2+
x+4,
直线AB的解析式为y=-
x+
,
得:B(5,4),C(0,4);
如图,设点D的横坐标为t(-3<t<5),
则点D的纵坐标为-
t2+
t+4.过点D作y轴的平行线交AB于E,
∴点E的坐标为(t,
t+
),
∴DE=(-
t2+
t+4)-(
t+
)=-
t2+
t+
,
∴S△DAB=
(-
t2+
t+
)×8=8,
解得t1=-1,t2=3,
∴D1(-1,3),D2(3,5).
 解:将A(-3,0)代入y=
解:将A(-3,0)代入y=| 1 |
| 2 |
| 2 |
| 5 |
得b=
| 3 |
| 2 |
| 1 |
| 6 |
则抛物线解析式为y=-
| 1 |
| 6 |
| 5 |
| 6 |
直线AB的解析式为y=-
| 1 |
| 2 |
| 3 |
| 2 |
得:B(5,4),C(0,4);
如图,设点D的横坐标为t(-3<t<5),
则点D的纵坐标为-
| 1 |
| 6 |
| 5 |
| 6 |
∴点E的坐标为(t,
| 1 |
| 2 |
| 3 |
| 2 |
∴DE=(-
| 1 |
| 6 |
| 5 |
| 6 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 6 |
| 1 |
| 3 |
| 5 |
| 2 |
∴S△DAB=
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 3 |
| 5 |
| 2 |
解得t1=-1,t2=3,
∴D1(-1,3),D2(3,5).
点评:考查的是用待定系数法求抛物线与直线的解析式.根据三角形的面积求动点坐标,主要是找到变化量、及不变量,进而得到动点坐标.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
已知ab<0,化简
的结果是( )
| ab2 |
A、b
| ||
B、-b
| ||
C、b
| ||
D、-b
|
能够判别一个四边形是平行四边形的条件是( )
| A、一组对角相等 |
| B、两条对角线互相垂直且相等 |
| C、两组对边分别相等 |
| D、一组对边平行 |
 如图,在△ABC中,∠ABC=45°,AD⊥BC于点D,点E在AD上,且BE=AC.求证:∠DEC=45°.
如图,在△ABC中,∠ABC=45°,AD⊥BC于点D,点E在AD上,且BE=AC.求证:∠DEC=45°.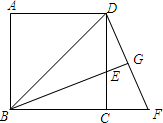 已知,如图,BD是正方形ABCD的对角线,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G,求证:
已知,如图,BD是正方形ABCD的对角线,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G,求证: 如图,已知△ABC中,AB的垂直平分线交BC于D,AC的垂直平分线交BC于E,M,N为垂足,若BD=3,DE=4,EC=5,求证:∠B=45°.
如图,已知△ABC中,AB的垂直平分线交BC于D,AC的垂直平分线交BC于E,M,N为垂足,若BD=3,DE=4,EC=5,求证:∠B=45°.