题目内容
梯形ABCD中，AB∥DC，AD=BC，EB⊥DC，若BE=AB，DB=DC=10，求AB的长？考点：梯形
专题：
分析：做AF⊥DC，设AB为x，进而表示出DF，DE的长，进而利用勾股定理求出即可．
解答：
解：做AF⊥DC，设AB为x，
则BE=AB=FE=x，DF=
，DE=
+x，
由勾股定理可知在直角三角形BED中，
x2+（
+x）2=102，
整理得：x2-4x-60=0，
解得：x1=10，x2=-6（不合题意舍去），
∴AB=6．
解：做AF⊥DC，设AB为x，则BE=AB=FE=x，DF=
| 10-x |
| 2 |
| 10-x |
| 2 |
由勾股定理可知在直角三角形BED中，
x2+（
| 10-x |
| 2 |
整理得：x2-4x-60=0，
解得：x1=10，x2=-6（不合题意舍去），
∴AB=6．
点评：此题主要考查了勾股定理以及等腰梯形的性质，根据题意表示出DF，DE的长是解题关键．
练习册系列答案
相关题目
?ABCD的周长为60cm，对角线交于点O，△BOC的周长比△AOB的周长小8cm，则AB，BC的长分别为（ ）
| A、18cm，10cm |
| B、19cm，11cm |
| C、20cm，12cm |
| D、34cm，26cm |
有下列方程：
①x2-2x=0；②9x2-25=0；③（2x-1）2=1；④
(x+3)2=27．
其中能用直接开平方法做的是（ ）
①x2-2x=0；②9x2-25=0；③（2x-1）2=1；④
| 1 |
| 3 |
其中能用直接开平方法做的是（ ）
| A、①②③ | B、②③ |
| C、②③④ | D、①②③④ |
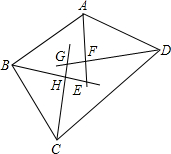四边形ABCD的四个内角的平分线两两相交叉形成一个四边形EFGH，求证：
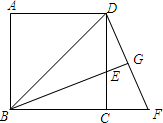已知，如图，BD是正方形ABCD的对角线，BE平分∠DBC，交DC于点E，延长BC到点F，使CF=CE，连接DF，交BE的延长线于点G，求证：