题目内容
15.观察下面的一组数据:1,5,14,30,55,…,根据上面数据显示的规律,第n个数可以表示为$\frac{n(n+1)(2n+1)}{6}$.分析 观察已知,每个数都是他的前序号个正整数平方和,由此可以得出第n个数为前n个正整数的平方和,利用前n项正整数平和和公式求出即可.
解答 解:根据已知:
第1个数:1=12,
第2个数:5=12+22,
第3个数:14=12+22+32,
第4个数:30=12+22+32+42,
第5个数:30=12+22+32+42+52,
…
∴第n个数:12+22+32+42+52+…+n2
=$\frac{n(n+1)(2n+1)}{6}$.
点评 题目考查了数字的变化规律,解决此类问题的关键是找出所求数字与序号的关系,另外要牢记前n项正整数的平方和为:$\frac{n(n+1)(2n+1)}{6}$,题目整体较为简单,适合随堂训练.

练习册系列答案
相关题目
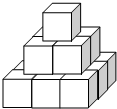 如图,把14个棱长为1cm的正方体木块,在地面上堆成如图所示的立体图形,然后向露出的表面部分喷漆,若1cm2需用漆2g,那么共需用漆84g.
如图,把14个棱长为1cm的正方体木块,在地面上堆成如图所示的立体图形,然后向露出的表面部分喷漆,若1cm2需用漆2g,那么共需用漆84g. 如图,已知平行四边形ABCD中,AB=2$\sqrt{5}$,AD=6,cot∠ABC=$\frac{1}{2}$,将边AB绕点A旋转,使得点B落在平行四边形ABCD的边上,其对应点为B′(点B′不与点B重合),那么sin∠CAB′=$\frac{\sqrt{10}}{10}$或$\frac{\sqrt{2}}{2}$.
如图,已知平行四边形ABCD中,AB=2$\sqrt{5}$,AD=6,cot∠ABC=$\frac{1}{2}$,将边AB绕点A旋转,使得点B落在平行四边形ABCD的边上,其对应点为B′(点B′不与点B重合),那么sin∠CAB′=$\frac{\sqrt{10}}{10}$或$\frac{\sqrt{2}}{2}$.
 如图,在△ABC中,∠C=90°,sinA=$\frac{2}{5}$,D为AC上一点,∠BDC=45°,DC=8,解直角△ABC.
如图,在△ABC中,∠C=90°,sinA=$\frac{2}{5}$,D为AC上一点,∠BDC=45°,DC=8,解直角△ABC. 如图,点P在圆O外,PA与圆O相切于A点,OP与圆周相交于C点,点B与点A关于直线PO对称,已知OA=4,∠POA=60°求:
如图,点P在圆O外,PA与圆O相切于A点,OP与圆周相交于C点,点B与点A关于直线PO对称,已知OA=4,∠POA=60°求: △ABC中,AB=AC=12厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为v厘米/秒,则当△BPD与△CQP全等时,v的值为2或3.
△ABC中,AB=AC=12厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为v厘米/秒,则当△BPD与△CQP全等时,v的值为2或3.