题目内容
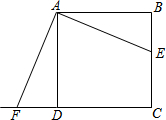如图，在边长为3cm的正方形ABCD中，点E为BC边上的任意一点，AF⊥AE，AF交CD的延长线于F，则四边形AFCE的面积为考点：全等三角形的判定与性质,正方形的性质
专题：
分析：由正方形ABCD中，AF⊥AE，易证得△BAE≌△DAF，即可得四边形AFCE的面积=正方形ABCD的面积，继而求得答案．
解答：解：∵四边形ABCD是正方形，
∴AD=AB，∠ADF=∠DAB=∠B=90°，
∴∠BAE+∠DAE=90°，
∵AF⊥AE，
∴∠DAF+∠DAE=90°，
∴∠BAE=∠DAF，
在△BAE和△DAF中，
，
∴△BAE≌△DAF（ASA），
∴S△BAE=S△DAF，
∴S四边形AFCE=S△DAF+S四边形ADCE=S△BAE+S四边形ADCE=S正方形=3×3=9（cm2）．
故答案为：9．
∴AD=AB，∠ADF=∠DAB=∠B=90°，
∴∠BAE+∠DAE=90°，
∵AF⊥AE，
∴∠DAF+∠DAE=90°，
∴∠BAE=∠DAF，
在△BAE和△DAF中，
|
∴△BAE≌△DAF（ASA），
∴S△BAE=S△DAF，
∴S四边形AFCE=S△DAF+S四边形ADCE=S△BAE+S四边形ADCE=S正方形=3×3=9（cm2）．
故答案为：9．
点评：此题考查了全等三角形的判定与性质以及正方形的性质．此题难度适中，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
如图，任意四边形ABCD各边中点分别是E、F、G、H，若对角线AC、BD的长都为10cm，则四边形EFGH的周长是
在如图的平面直角坐标系中，有一条通过点（-3，-2）的直线l．若四点（-2，a），（0，b），（c，0），（d，-1）在直线l上，则（a-b）c-d）若|2-a|+
=0，则a+b的值是（ ）
| 3+b |
| A、2 | B、0 | C、1 | D、-1 |
如图，正方形ABCD中，AB=4cm，点M、P分别从D、B两点同时出发，以1.5cm/s、1cm/s的速度沿DA、BC运动；点N从A点以3cm/s的速度也同时出发，沿AB、BC运动，当点N到达点C时，点N、M、P同时停止运动，设运动时间为t（s）；△MNP的面积为s（cm2），则s（cm2）与t（s）的函数关系可用图象表示为（ ）
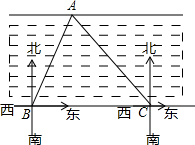如图，某施工单位为测得某河段的宽度，测量员先在河对岸边取一点A，再在河这边沿河边取两点B、C，在点B处测得A在北偏东30°方向上，在点C处测得点A在西北方向上，量得BC长为400米，请你求出该河段的宽度．（结果保留根号）