题目内容
 在如图的平面直角坐标系中,有一条通过点(-3,-2)的直线l.若四点(-2,a),(0,b),(c,0),(d,-1)在直线l上,则(a-b)c-d)
在如图的平面直角坐标系中,有一条通过点(-3,-2)的直线l.若四点(-2,a),(0,b),(c,0),(d,-1)在直线l上,则(a-b)c-d)考点:一次函数图象上点的坐标特征
专题:
分析:设出函数解析式为y=kx+b,将(-3,-2),(-2,a),(c,0),(d,-1)分别代入解析式,将③-②的值与④的变式组合即可求出(a-b)(c-d)=-2k•
=-2<0.
| 1 |
| k |
解答:解:设函数解析式为y=kx+b,
将(-3,-2),(-2,a),(c,0),(d,-1)分别代入解析式得,
,
③-②得,(c-d)k=1,c-d=
;
由④得,a-b=-2k,
(a-b)(c-d)=-2k•
=-2<0.
故答案为:<.
将(-3,-2),(-2,a),(c,0),(d,-1)分别代入解析式得,
|
③-②得,(c-d)k=1,c-d=
| 1 |
| k |
由④得,a-b=-2k,
(a-b)(c-d)=-2k•
| 1 |
| k |
故答案为:<.
点评:本题考查了一次函数图象上点的坐标特征,要知道经过函数的某点一定在函数的图象上.

练习册系列答案
相关题目
 函数y=kx+b(k、b为常数,k≠0)的图象如图,则关于x的不等式kx+b>0的解集为( )
函数y=kx+b(k、b为常数,k≠0)的图象如图,则关于x的不等式kx+b>0的解集为( )| A、x>0 | B、x<0 |
| C、x<2 | D、x>2 |
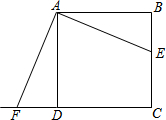 如图,在边长为3cm的正方形ABCD中,点E为BC边上的任意一点,AF⊥AE,AF交CD的延长线于F,则四边形AFCE的面积为
如图,在边长为3cm的正方形ABCD中,点E为BC边上的任意一点,AF⊥AE,AF交CD的延长线于F,则四边形AFCE的面积为