题目内容
 如图,正方形ABCD中,AB=4cm,点M、P分别从D、B两点同时出发,以1.5cm/s、1cm/s的速度沿DA、BC运动;点N从A点以3cm/s的速度也同时出发,沿AB、BC运动,当点N到达点C时,点N、M、P同时停止运动,设运动时间为t(s);△MNP的面积为s(cm2),则s(cm2)与t(s)的函数关系可用图象表示为( )
如图,正方形ABCD中,AB=4cm,点M、P分别从D、B两点同时出发,以1.5cm/s、1cm/s的速度沿DA、BC运动;点N从A点以3cm/s的速度也同时出发,沿AB、BC运动,当点N到达点C时,点N、M、P同时停止运动,设运动时间为t(s);△MNP的面积为s(cm2),则s(cm2)与t(s)的函数关系可用图象表示为( )A、 |
B、 |
C、 |
D、 |
考点:圆锥的计算
专题:
分析:求出每段的函数解析式,根据函数的性质即可作出判断.
解答:解:当N在AB上是,0<t<
秒时,s=4×4-
(4-1.5t+4-t)×4-
(4-1.5t)×3t-
(4-3t)×t,
即s=
t2-3t,对称轴是x=
,故B、C、D错误;
当t>
时,N在BC上,s=
×4×【(3t-4)-t】,即s=4t-8,是一次函数,当t=2时,s=0.
故选A.
| 4 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |

即s=
| 15 |
| 4 |
| 2 |
| 5 |
当t>
| 4 |
| 3 |
| 1 |
| 2 |
故选A.
点评:本题考查了求函数的解析式以及函数的图象,正确求得函数的解析式是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 函数y=kx+b(k、b为常数,k≠0)的图象如图,则关于x的不等式kx+b>0的解集为( )
函数y=kx+b(k、b为常数,k≠0)的图象如图,则关于x的不等式kx+b>0的解集为( )| A、x>0 | B、x<0 |
| C、x<2 | D、x>2 |
 如图,AB∥MP∥CD,MN平分∠AMD,∠A=40°,∠D=60°,那么∠NMP的度数是( )
如图,AB∥MP∥CD,MN平分∠AMD,∠A=40°,∠D=60°,那么∠NMP的度数是( )| A、40° | B、30° |
| C、20° | D、10° |
 如图是一个由7个同样的正方体组成的一个立体图形,它的左视图是( )
如图是一个由7个同样的正方体组成的一个立体图形,它的左视图是( )A、 |
B、 |
C、 |
D、 |
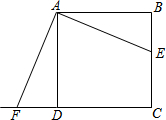 如图,在边长为3cm的正方形ABCD中,点E为BC边上的任意一点,AF⊥AE,AF交CD的延长线于F,则四边形AFCE的面积为
如图,在边长为3cm的正方形ABCD中,点E为BC边上的任意一点,AF⊥AE,AF交CD的延长线于F,则四边形AFCE的面积为